题目内容
经过椭圆
+y2=1的左焦点F1作倾斜角为60°的直线l,直线l与椭圆相交于A,B两点,求AB的长.
| x2 |
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆的左焦点F1(-1,0),根据点斜率式设AB,方程与椭圆方程消去y,利用根与系数的关系,根据弦长公式即可算出弦AB的长.
解答:
解:∵椭圆方程为
+y2=1,
∴焦点分别为F1(-1,0),F2(1,0),
∵直线AB过左焦点F1倾斜角为60°,
∴直线AB的方程为y=
(x+1),
将AB方程与椭圆方程消去y,得7x2+12x+4=0
设A(x1,y1),B(x2,y2),可得
x1+x2=-
,x1x2=
∴|x1-x2|=
=
因此,|AB|=
•|x1-x2|=
.
| x2 |
| 2 |
∴焦点分别为F1(-1,0),F2(1,0),
∵直线AB过左焦点F1倾斜角为60°,
∴直线AB的方程为y=
| 3 |
将AB方程与椭圆方程消去y,得7x2+12x+4=0
设A(x1,y1),B(x2,y2),可得
x1+x2=-
| 12 |
| 7 |
| 4 |
| 7 |
∴|x1-x2|=
(-
|
4
| ||
| 7 |
因此,|AB|=
| 1+3 |
8
| ||
| 7 |
点评:本题给出椭圆经过左焦点且倾角为30度的弦AB,求弦长.着重考查了椭圆的标准方程与简单几何性质、直线与椭圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
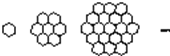 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数. 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<