题目内容
在等边△ABC中,M,N分别为AB,AC上的点,满足AM=AN=2,沿MN将△AMN折起,使得平面AMN与平面MNCB所成的二面角为60°,则A点到平面MNCB的距离为 .
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:取MN的中点O,连接AO,OP,则∠AOP=60°,求出AO,即可求出A点到平面MNCB的距离.
解答:
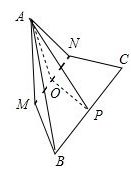 解:取MN的中点O,连接AO,OP,则∠AOP=60°
解:取MN的中点O,连接AO,OP,则∠AOP=60°
∵AM=AN=2,
∴AO=
∴A点到平面MNCB的距离为AOsin60°=
.
故答案为:
.
 解:取MN的中点O,连接AO,OP,则∠AOP=60°
解:取MN的中点O,连接AO,OP,则∠AOP=60°∵AM=AN=2,
∴AO=
| 3 |
∴A点到平面MNCB的距离为AOsin60°=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查空间角,考查点到平面的距离,考查学生的计算能力,确定空间角是关键.

练习册系列答案
相关题目
函数f(x)=x3+x-1在(0,4)上零点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
二次函数f(x)=ax2+bx+c(x∈R)的部分对应值如下表:
可以判断方程ax2+bx+c=0的两个根所在的区间是( )
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | M | -4 | -6 | -6 | -4 | n | 6 |
| A、(-3,-1)和(2,4) |
| B、(-3,-1)和(-1,1) |
| C、(-1,1)和(1,2) |
| D、(-∞,-3)和(4,+∞) |
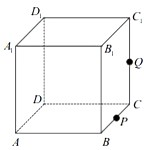 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是