题目内容
已知等比数列{an}的前n项和Sn=t•5n-2-
,则实数t的值为( )
| 1 |
| 5 |
| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:由题意可得a1,a2,a3的值,根据等比数列的定义可得t的方程,解方程可得.
解答:
解:由题意可得 a1=S1=
t-
,
a2=S2-S1=
t,a3=S3-S2=4t,
∴(
t)2=(
t-
)•4t,
解得t=5,或t=0(舍去)
故选:B
| 1 |
| 5 |
| 1 |
| 5 |
a2=S2-S1=
| 4 |
| 5 |
∴(
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
解得t=5,或t=0(舍去)
故选:B
点评:本题考查等比数列的定义和性质,求出等比数列的前三项是解题的关键,属基础题.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
在△ABC中,内角A,B,C的对边分别为a,b,c.若a=2,b+c=7,cosB=-
,则c=( )
| 1 |
| 4 |
| A、3 | B、4 | C、5 | D、6 |
下列判断正确的是( )
A、函数f(x)=
| ||
| B、函数f(x)=x2-|x|是偶函数 | ||
| C、函数f(x)=x0是非奇非偶函数 | ||
| D、函数f(x)=2既是奇函数又是偶函数 |
已知复数z满足
=i(i为虚数单位),则z的值为( )
| 1+z |
| 1-z |
| A、i | B、-i | C、1 | D、-1 |
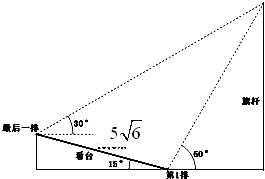 某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5