Question

已知O为坐标原点，A，B两点的坐标均满足不等式组

x-3y+1≤0 x+y-3≤0 x-1≥0

，设

OA

与

OB

的夹角为θ，则tanθ的最大值为（　　）

• A、

  1

  2

• B、

  4

  7

• C、

  3

  4

• D、

  9

  4

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，利用数形结合求出A，B的位置，利用向量的数量积求出夹角的余弦，即可得到结论．

解答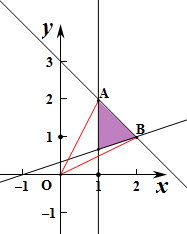： 解：作出不等式组对应的平面区域，要使tanθ最大，
则由

x=1 x+y-3=0

，得

x=1 y=2

，即A（1，2），
由

x-3y+1=0 x+y-3=0

，得

x=2 y=1

，即B（2，1），
∴此时夹角θ最大，
则

OA

=(1，2)，

OB

=(2，1)，
则cosθ=

OA • OB

| OA |•| OB |

=

2+2

5 • 5

=

4

5

，
∴sinθ=

3

5

，
此时tanθ=

sinθ

cosθ

=

3

4

，
故选：C．

点评：本题主要考查线性规划的应用，以及向量的数量积运算，利用数形结合是解决本题的关键．