题目内容
已知等差数列{an}的前m项和为100，前3m项的和为-150，则它的前2m项的和为（ ）
| A、25 | B、-25 | C、50 | D、75 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的性质得Sm，S2m-Sm，S3m-S2m成等差数列，从而得到2（S2m-100）=100+（-150-S2m），由此能求出它的前2m项的和．
解答：
解：∵等差数列{an}的前m项和为100，前3m项的和为-150，
又Sm，S2m-Sm，S3m-S2m成等差数列，
∴100，S2m-100，-150-S2m成等差数列，
∴2（S2m-100）=100+（-150-S2m），
解得S2m=50．
故选：C．
又Sm，S2m-Sm，S3m-S2m成等差数列，
∴100，S2m-100，-150-S2m成等差数列，
∴2（S2m-100）=100+（-150-S2m），
解得S2m=50．
故选：C．
点评：本题考查等差数列的前2m项的和的求法，是基础题，解题时要注意等差数列的性质的合理运用．
练习册系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，且f（2+x）=f（2-x），则f（4）=（ ）
| A、4 | B、2 | C、0 | D、不确定 |
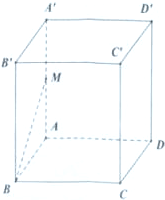如图，在直平行六面体ABCD-A′B′C′D′中，底面ABCD是边长为2的菱形，∠ABC=60°，A′C与底面ABCD所成角的大小为arctan2，M为A′A的中点．