题目内容
设集合A={-1，1，2}，B={a+1，a2+3}，A∩B={2}，则实数a的值为（ ）
| A、1 | B、2 | C、3 | D、0 |
考点：交集及其运算
专题：集合
分析：由A，B，以及A与B的交集，确定出a的值即可．
解答：
解：∵A={-1，1，2}，B={a+1，a2+3}，A∩B={2}，
∴2∈B，即a+1=2或a2+3=2，
解得：a=1，
故选：A．
∴2∈B，即a+1=2或a2+3=2，
解得：a=1，
故选：A．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
若点P到点F（0，2）的距离比它到直线y+4=0的距离小2，则P的轨迹方程为（ ）
| A、y2=8x |
| B、y2=-8x |
| C、x2=8y |
| D、x2=-8y |
正方体ABCD-A′B′C′D′中，和AB垂直的棱的条数是（ ）
| A、4 | B、6 | C、8 | D、10 |
已知一空间几何体的三视图如图所示，该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、14 |
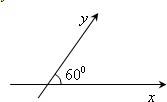如图，在平面斜坐标系xoy中，∠xoy=60°，平面上任一点P在斜坐标系中的斜坐标是这样定义的：若
| OP |
轴方向相同的单位向量），则P点的斜坐标为（x，y）．若P点的斜坐标为（3，-4），则点P到原点O的距离|PO|=（ ）
A、
| ||
B、3
| ||
| C、5 | ||
D、
|