题目内容
如图为某几何体的三视图，则其体积为（ ）
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知几何体是：底面为直角三角形一条侧棱垂直底面直角顶点的三棱锥，列出体积表达式，可求几何体的体积．
解答：
解：几何体是：底面为直角三角形一条侧棱垂直底面直角顶点的三棱锥，
PA=1，AB=2，AC=2，
V=
×（
×2×2）×1=
，
故选：D．
PA=1，AB=2，AC=2，
V=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
故选：D．
点评：本小题考查由三视图求体积，考查了简单几何体的三视图的运用．培养同学们的空间想象能力和基本的运算能力．是中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
若将长为6的一条线段分成长度为正整数的三条线段，则这三条线段可以构成三角形的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合M={1，2，a}，N={b，2}，M∩N={2，3}，则M∪N=（ ）
| A、{1，3} |
| B、{2，3} |
| C、{1，2} |
| D、{1，2，3} |
若点P到点F（0，2）的距离比它到直线y+4=0的距离小2，则P的轨迹方程为（ ）
| A、y2=8x |
| B、y2=-8x |
| C、x2=8y |
| D、x2=-8y |
在等比数列{an}中，a4，a12是方程x2+2011x+121=0的两根，则a8的值为（ ）
| A、11 | ||
| B、-11 | ||
| C、±11 | ||
D、
|
已知sin（
-x）=
，则sin2x的值为（ ）
| π |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、±
|
设点M（x0，1），若在圆O：x2+y2=1上存在点N，使得∠OMN=30°，则x0的取值范围是（ ）
A、[-
| ||||||||
B、[-
| ||||||||
| C、[-2，2] | ||||||||
D、[-
|
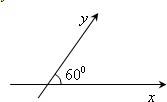如图，在平面斜坐标系xoy中，∠xoy=60°，平面上任一点P在斜坐标系