题目内容
椭圆C:
+
=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,在x轴负半轴上有一点B,满足
=
,AB⊥AF2.
(Ⅰ)求椭圆C的离心率.
(Ⅱ)D是过A,B,F2三点的圆上的点,D到直线l:x-
y-3=0的最大距离等于椭圆长轴的长,求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
(Ⅰ)求椭圆C的离心率.
(Ⅱ)D是过A,B,F2三点的圆上的点,D到直线l:x-
| 3 |
考点:椭圆的简单性质,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(I)设B(x0,0),由F1(-c,0),F2(c,0),A(0,b),由
=
,可得x0=-3c.由AB⊥AF2,可得
•
=-3c2+b2=0,再利用a2=b2+c2.即可得出.
(II)由(1)知
=
,得c=
a.由题意知△ABF2为直角三角形,BF2为斜边,△ABF2的外接圆圆心为F1(-
a,0),半径r=a.D到直线l:x-
y-3=0的最大距离等于2a,圆心到直线的距离为a,利用点到直线的距离公式即可得出.
| BF1 |
| F1F2 |
| AB |
| AF2 |
(II)由(1)知
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解答:
解:(I)设B(x0,0),由F1(-c,0),F2(c,0),A(0,b),
∵满足
=
,
∴(-c-x0,0)=(2c,0),∴-c-x0=2c.
解得x0=-3c.
∵AB⊥AF2,
=(-3c,-b),
=(c,-b).
∴
•
=-3c2+b2=0,
∴a2=b2+c2=4c2.
∴a=2c.
故椭圆C的离心率e=
.
(II)由(1)知
=
,得c=
a.
可得B(-
a,0),F2(
a,0).
由题意知△ABF2为直角三角形,BF2为斜边,
∴△ABF2的外接圆圆心为F1(-
a,0),半径r=a.
D到直线l:x-
y-3=0的最大距离等于2a,
∴圆心到直线的距离为a,
∴
=a,解得a=2,
解得c=1,b=
.
∴椭圆C的方程为
+
=1.
∵满足
| BF1 |
| F1F2 |
∴(-c-x0,0)=(2c,0),∴-c-x0=2c.
解得x0=-3c.
∵AB⊥AF2,
| AB |
| AF2 |
∴
| AB |
| AF2 |
∴a2=b2+c2=4c2.
∴a=2c.
故椭圆C的离心率e=
| 1 |
| 2 |
(II)由(1)知
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
可得B(-
| 3 |
| 2 |
| 1 |
| 2 |
由题意知△ABF2为直角三角形,BF2为斜边,
∴△ABF2的外接圆圆心为F1(-
| 1 |
| 2 |
D到直线l:x-
| 3 |
∴圆心到直线的距离为a,
∴
|-
| ||||
|
解得c=1,b=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题考查了椭圆的标准方程及其性质、三角形的外接圆的性质、点到直线的距离公式、直角三角形的性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=30°,则x0的取值范围是( )
A、[-
| ||||||||
B、[-
| ||||||||
| C、[-2,2] | ||||||||
D、[-
|
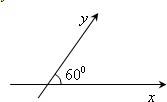 如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系
如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系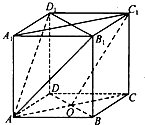 如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.
如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.