题目内容
已知公差不为0的等差数列{an}中,a1=2,{an}部分项按原来的顺序由小到大组成等比数列{akn},且k1=1,k2=3,k3=11.
(1)求该等比数列的公比q;
(2)求akn及kn.
(1)求该等比数列的公比q;
(2)求akn及kn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:根据等差数列和等比数列的通项公式分别求出对应的公差和公比,即可得到结论.
解答:
解:(1)∵数列{an}为等差数列,首项a1=2,公差d≠0,{an}部分项按原来的顺序由小到大组成等比数列{akn},且k1=1,k2=3,k3=11.
∴a1•a11=
,
即(2+2d)2=2•(2+10d),
解得d=3,
即an=2+3(n-1)=3n-1,
∴q=
=
=4.
(2)由(1)得akn=3kn-1=2×4n-1=22n-1,
∴kn=
.
∴a1•a11=
| a | 2 3 |
即(2+2d)2=2•(2+10d),
解得d=3,
即an=2+3(n-1)=3n-1,
∴q=
| a3 |
| a1 |
| 3×3-1 |
| 2 |
(2)由(1)得akn=3kn-1=2×4n-1=22n-1,
∴kn=
| 22n-1+1 |
| 3 |
点评:本题主要考查数列通项公式的计算,利用等差数列和等比数列的定义和通项公式求出公比和公差是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知椭圆
+
=1(a>b>0)上一点A关于原点的对称点为点B,F为其右焦点,若AF⊥BF,设∠ABF=α,且α∈[
,
],则该椭圆离心率e的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| π |
| 4 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
设f(x)=x3-
x2-2x+5,当x∈[-1,2]时,f(x)<m恒成立,则实数m的取值范围为( )
| 1 |
| 2 |
| A、m>7 | ||
B、m>
| ||
C、
| ||
| D、m<7 |
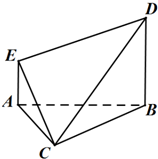 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1.