题目内容
若sin（α-π）=2cos（α-2π），求
的值．
| sin(7π-α)+5cos(2π-α) | ||
3sin(
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：利用诱导公式可得tanα=-2，再将所求关系式中的“弦”化“切”，将得tanα=-2代入即可求得答案．
解答：
解：∵sin（α-π）=2cos（α-2π），
∴-sinα=2cosα，
∴tanα=-2；
∴原式=
=
=
=-1．
∴-sinα=2cosα，
∴tanα=-2；
∴原式=
| sinα+5cosα |
| -3cosα+sinα |
| tanα+5 |
| tanα-3 |
| -2+5 |
| -2-3 |
点评：本题考查运用诱导公式化简求值，求得tanα=-2，将所求关系式中的“弦”化“切”是关键，属于中档题．
练习册系列答案
相关题目
f（x）=2x+3x的一个零点所在的一个区间是 （ ）
| A、（1，2） |
| B、（0，1） |
| C、（-1，0） |
| D、（-2，-1） |
如图，在平面直角坐标系xOy中，点A（x1，y1）在单位圆O上，∠xOA=α，且α∈（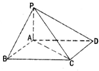
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠ABC=60°，BC=2AB，PA⊥底面ABCD．