题目内容
复数z1=1+bi，z2=-2+i，若
的实部和虚部互为相反数，则实数b的值为（ ）
| z1 |
| z2 |
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：化简复数
为a+bi（a、b∈R）的形式，实部和虚部互为相反数，可得实数b的值．
| z1 |
| z2 |
解答：
解：复数z1=1+bi，z2=-2+i，
=
=
=
，
∵
的实部和虚部互为相反数，
∴b-2=2b+1，
解得b=-3．
故选：D．
| z1 |
| z2 |
| 1+bi |
| -2+i |
| (1+bi)(-2-i) |
| (-2+i)(-2-i) |
| (b-2)+(-2b-1)i |
| 5 |
∵
| z1 |
| z2 |
∴b-2=2b+1，
解得b=-3．
故选：D．
点评：本题考查复数代数形式的混合运算，复数的基本概念的应用，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设x0是函数f（x）=x
-3的零点，则x0的值是（ ）
| 1 |
| 2 |
| A、4 | B、8 | C、9 | D、16 |
设曲线y=
与x轴所围成的区域为D，向区域D内随机投一点，则该点落入区域{（x，y）∈D|x2+y2＜2}的概率是（ ）
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[-2，0]时，f（x）=（
）x-1，若在区间（-2，6）内，函数y=f（x）-loga（x+2），（a＞0，a≠1）恰有1个零点，则实数a的取值范围是（ ）
| ||
| 2 |
| A、（1，4） | ||
| B、（4，+∞） | ||
C、（
| ||
| D、（0，1）∪（1，4） |
i为虚数，则复数（-1+i）（1+i）=（ ）
| A、-2+i | B、-2 |
| C、-1+i | D、-1 |
已知
=（2，1），
=（-1，k），如果
∥
，则实数k的值等于（ ）
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
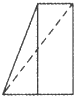
如图甲，将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD，得到几何体BCDEF，如图乙，则该几何体的正视图（或称主视图）是（ ）
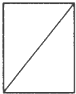
已知椭圆C1：