题目内容
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f″(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数f(x)=ax3+bx2+cx+d(a≠0)都关于点(-
,f(-
))对称:
②存在三次函数f(x)=ax3+bx2+cx+d(a≠0),若f′(x)=0有实数解x0,则点(x0,f(x0))为函数y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)=
x3-
x2-
,则:g(
)+g(
)+g(
)+…+g(
)=-1005.5
其中所有正确结论的序号是( )
①任意三次函数f(x)=ax3+bx2+cx+d(a≠0)都关于点(-
| b |
| 3a |
| b |
| 3a |
②存在三次函数f(x)=ax3+bx2+cx+d(a≠0),若f′(x)=0有实数解x0,则点(x0,f(x0))为函数y=f(x)的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2012 |
| 2 |
| 2012 |
| 3 |
| 2012 |
| 2011 |
| 2012 |
其中所有正确结论的序号是( )
| A、①②④ | B、①②③ |
| C、①③④ | D、②③④ |
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:①根据函数f(x)的解析式求出f′(x)和f″(x),令f″(x)=0,求得x的值,由此求得三次函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心;
②③利用三次函数对称中心的定义和性质进行判断;
④由g(x)=
x3-
x2-
的对称中心是(
,-
),得g(x)+(g(1-x)=-1,由此能求出g(
)+g(
)+g(
)+…+g(
)的值.
②③利用三次函数对称中心的定义和性质进行判断;
④由g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2012 |
| 2 |
| 2012 |
| 3 |
| 2012 |
| 2011 |
| 2012 |
解答:
解:∵f(x)=ax3+bx2+cx+d(a≠0),
∴f′(x)=3ax2+2bx+c,f''(x)=6ax+2b,
∵f″(x)=6a×(-
)+2b=0,
∴任意三次函数都关于点(-
,f(-
))对称,即①正确;
∵任何三次函数都有对称中心,且“拐点”就是对称中心,
∴存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为y=f(x)的对称中心,即②正确;
任何三次函数都有且只有一个对称中心,故③不正确;
∵g(x)=
x3-
x2-
,
∴g′(x)=x2-x,g''(x)=2x-1,
令g''(x)=2x-1=0,得x=
,
∵g(
)=
×(
)3-
×(
)2-
=-
,
∴函数g(x)=
x3-
x2-
的对称中心是(
,-
),
∴g(x)+g(1-x)=-1,
∴g(
)+g(
)+g(
)+…+g(
)=-1005.5,故④正确.
故正确结论为:①②④.
故选:A
∴f′(x)=3ax2+2bx+c,f''(x)=6ax+2b,
∵f″(x)=6a×(-
| b |
| 3a |
∴任意三次函数都关于点(-
| b |
| 3a |
| b |
| 3a |
∵任何三次函数都有对称中心,且“拐点”就是对称中心,
∴存在三次函数f′(x)=0有实数解x0,点(x0,f(x0))为y=f(x)的对称中心,即②正确;
任何三次函数都有且只有一个对称中心,故③不正确;
∵g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
∴g′(x)=x2-x,g''(x)=2x-1,
令g''(x)=2x-1=0,得x=
| 1 |
| 2 |
∵g(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
∴函数g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
∴g(x)+g(1-x)=-1,
∴g(
| 1 |
| 2012 |
| 2 |
| 2012 |
| 3 |
| 2012 |
| 2011 |
| 2012 |
故正确结论为:①②④.
故选:A
点评:本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,求函数的值以及函数的对称性的应用,属于难题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知全集U={0,1,2,3,4},集合A={1,3,4},B={2,3},则A∩(∁UB)为( )
| A、{3} | B、{0,2} |
| C、∅ | D、{1,4} |
设x0是函数f(x)=x
-3的零点,则x0的值是( )
| 1 |
| 2 |
| A、4 | B、8 | C、9 | D、16 |
执行如图的程序框图,输出的结果是( )
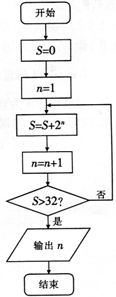

| A、3 | B、4 | C、5 | D、6 |
已知集合A={x||x-2|>2},B={x|x∈N},则(∁UA)∩B=( )
| A、{1,2,3} |
| B、{0,1,2,3} |
| C、{0,1,2,3,4} |
| D、{1,2,3,4} |
方程log3x=x-3的根的情况是( )
| A、仅有一个正实数根 |
| B、有两个负根 |
| C、有一个正根和一个负根 |
| D、有两个正根 |
设曲线y=
与x轴所围成的区域为D,向区域D内随机投一点,则该点落入区域{(x,y)∈D|x2+y2<2}的概率是( )
| 2x-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正视图(或称主视图)是( )
如图甲,将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD,得到几何体BCDEF,如图乙,则该几何体的正视图(或称主视图)是( )