题目内容
13．已知点P（x，y）在不等式组$\left\{\begin{array}{l}2x-y+a≥0\\ 3x+y-3≤0\end{array}\right.$（a为常数）表示的平面区域上运动，若z=4x+3y的最大值为8，则a=2．分析 由题意，求不等式组对应的方程组得交点P的坐标，利用交点P在不等式组表示的区域上运动时z=4x+3y的最大值为8，求出a的值．
解答 解：由题意，由方程组$\left\{\begin{array}{l}{2x-y+a=0}\\{3x+y-3=0}\end{array}\right.$（a为常数），
可得交点（$\frac{3-a}{5}$，$\frac{6+3a}{5}$），
当点P（x，y）在不等式组$\left\{\begin{array}{l}2x-y+a≥0\\ 3x+y-3≤0\end{array}\right.$表示的区域上运动时，
z=4x+3y的最大值为8，
∴4×$\frac{3-a}{5}$+3×$\frac{6+3a}{5}$=8，
解得a=2．
故答案为：2．
点评 本题考查了二元一次不等式组表示平面区域的应用问题，也考查了求最值的问题，是中档题．
练习册系列答案
相关题目
3．为调查高中生的数学成绩与学生自主学习时间之间的相关关系，某重点高中数学教师对新入学的45名学生进行了跟踪调查，其中每周自主做数学题时间不少于15小时的有19人，余下的人中，在高三模拟考试中数学平均成绩不足120分的占$\frac{8}{13}$，统计成绩后，得到如下的2×2列联表：
（Ⅰ）请完成上面的2×2列联表，并判断在“犯错误概率不超过0.01”的前提下，能否认为“高中生的数学成绩与学生自主学习时间之间有相关关系”；
（Ⅱ）按照分层抽样的方法，在上述样本中，从分数大于等于120分和分数不足120分的两组学生中抽取9名学生，若在上述9名学生中随机抽取2人，求至少1人分数不足120分的概率．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
| 分数大于等于120分 | 分数不足120分 | 合计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合计 | 25 | 20 | 45 |
（Ⅱ）按照分层抽样的方法，在上述样本中，从分数大于等于120分和分数不足120分的两组学生中抽取9名学生，若在上述9名学生中随机抽取2人，求至少1人分数不足120分的概率．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
| P（K2≥k0） | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
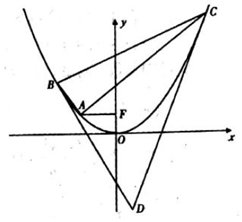如图，点F是抛物线τ：x2=2py （p＞0）的焦点，点A是抛物线上的定点，且$\overrightarrow{AF}$=（2，0），点B，C是抛物线上的动点，直线AB，AC斜率分别为k1，k2．
3．已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$，则其焦距为（ ）
| A． | $\sqrt{5}$ | B． | $2\sqrt{5}$ | C． | $\sqrt{13}$ | D． | $2\sqrt{13}$ |