题目内容
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域.
(2)求f(x)在区间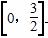 上的最大值.
上的最大值.
解:∵f(1)=2,∴loga4=2(a>0,a≠1),
∴a=2.
由 得x∈(-1,3),
得x∈(-1,3),
∴函数f(x)的定义域为 (-1,3).
(2)f(x)=log2(1+x)+log2(3-x)=
log2(1+x)(3-x)=log2[-(x-1)2+4],
∴当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
函数f(x)在 上的最大值是f(1)=log24=2.
上的最大值是f(1)=log24=2.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知函数y=f(x)的图像是连续不间断的曲线,且有如下的对应值:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 124.4 | 35 | -74 | 14.5 | -56.7 | -123.6 |
则函数y=f(x)在区间[1,6]上的零点至少有( )
A.2个 B.3个
C.4个 D.5个
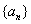 满足
满足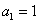 ,
,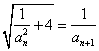 ,记数列
,记数列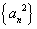 前n项的和为Sn,若
前n项的和为Sn,若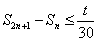 对任意的
对任意的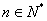 恒成立,则正整数
恒成立,则正整数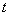 的最小值为 ( )
的最小值为 ( )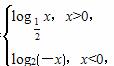 若f(m)<f(-m),则实数m的取值范围是( )
若f(m)<f(-m),则实数m的取值范围是( )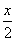 +
+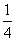 .证明:存在x0∈
.证明:存在x0∈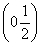 ,使f(x0)=x0.
,使f(x0)=x0. 与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )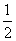 D.1
D.1