题目内容
13.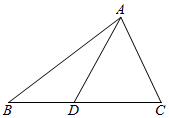 如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.
如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.(I)求cos∠CAD;
(Ⅱ)求线段AD的长.
分析 (I)在△ABC中使用余弦定理解出C,再在△ACD中利用内角和定理得出cos∠CAD;
(II)在△ACD中使用正弦定理求出AD.
解答 解:(I)在△ABC中,由余弦定理得cosC=$\frac{A{C}^{2}+B{C}^{2}-A{B}^{2}}{2AC•BC}$=$\frac{1}{3}$.∴sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{2\sqrt{2}}{3}$.
∵∠ADB=120°,∴∠ADC=60°.
∴cos∠CAD=-cos(C+60°)=sinCsin60°-cosCcos60°=$\frac{2\sqrt{6}-1}{6}$.
(II)在△ACD中,由正弦定理得$\frac{AC}{sin∠ADC}=\frac{AD}{sinC}$,
即$\frac{3\sqrt{6}}{\frac{\sqrt{3}}{2}}=\frac{AD}{\frac{2\sqrt{2}}{3}}$,解得AD=8.
点评 本题考查了正余弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
18.在△ABC中,若${a^2}-{b^2}=\sqrt{3}bc$且$\frac{c}{b}=2\sqrt{3}$,则角A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
5.若点M(3,1)、N(-1,3)均在直线ax-y+2=0的同一侧,则实数a的取值范围是( )
| A. | $(-1,-\frac{1}{3})$ | B. | $(\frac{1}{3},1)$ | C. | $(-∞,-1)∪(-\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})∪(1,+∞)$ |
3.已知:幂函数y=x3m-7(m∈N*)在区间(0,+∞)内为减函数,且幂函数的图象关于y轴对称,则m等于( )
| A. | -4 | B. | 1或2 | C. | 1 | D. | 2 |



