题目内容
1.已知f(x)=$\sqrt{3}$cos2ωx+sinωxcosωx-1(ω>0)的最小正周期是$\frac{π}{2}$,求:(1)ω的值;
(2)函数f(x)的最大值和使f(x)取得最大值的x的集合.
分析 (1)由三角函数公式化简可得f(x)=sin(2ωx+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$-1,由周期公式可得ω的方程,解方程可得ω值;
(2)当4x+$\frac{π}{3}$=2kπ+$\frac{π}{2}$k∈Z时,函数取最大值$\frac{\sqrt{3}}{2}$,变形可得此时x集合.
解答 解:(1)由三角函数公式化简可得
f(x)=$\sqrt{3}$cos2ωx+sinωxcosωx-1
=$\frac{\sqrt{3}}{2}$(1+cos2ωx)+$\frac{1}{2}$sin2ωx-1
=$\frac{\sqrt{3}}{2}$cos2ωx+$\frac{1}{2}$sin2ωx+$\frac{\sqrt{3}}{2}$-1
=sin(2ωx+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$-1
∵函数f(x)最小正周期是$\frac{π}{2}$,
∴$\frac{2π}{2ω}$=$\frac{π}{2}$,解得ω=2;
(2)由(1)可得f(x)=sin(4x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$-1
当4x+$\frac{π}{3}$=2kπ+$\frac{π}{2}$即x=$\frac{kπ}{2}$+$\frac{π}{24}$,k∈Z时,函数取最大值$\frac{\sqrt{3}}{2}$,
此时x的集合为{x|x=$\frac{kπ}{2}$+$\frac{π}{24}$,k∈Z}
点评 本题考查三角函数的最值,涉及三角函数的周期公式,属基础题.

练习册系列答案
相关题目
12.${(x-\frac{a}{x})^5}(x∈R)$展开式中x3的系数为10,则实数a的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | -2 |
6.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在一点P(非左、右顶点)使$\frac{a}{|P{F}_{2}|}$=$\frac{c}{|P{F}_{1}|}$,该椭圆的离心率取值范围为( )
| A. | ($\sqrt{2}-1$,1) | B. | [$\sqrt{2}$-1,1) | C. | (2-$\sqrt{2}$,1) | D. | [2-$\sqrt{2}$,1) |
10.已知方程(x2-mx+4)(x2-nx+4)=0的四个根组成一个首项$\frac{1}{4}$的等比数列,则|m-n|的值为( )
| A. | 0 | B. | $11\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
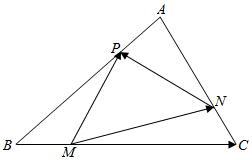 如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.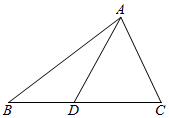 如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.
如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.