题目内容
3.已知:幂函数y=x3m-7(m∈N*)在区间(0,+∞)内为减函数,且幂函数的图象关于y轴对称,则m等于( )| A. | -4 | B. | 1或2 | C. | 1 | D. | 2 |
分析 根据幂函数的单调性列出不等式,由m∈N*求出m的值,并分别求出函数的解析式,判断函数的图象是否关于y轴对称,即可得到答案.
解答 解:因为幂函数y=x3m-7(m∈N*)在区间(0,+∞)内为减函数,
所以3m-7<0,则m<$\frac{7}{3}$,
又m∈N*,则m可能是1、2,
当m=1时,y=x3m-7=y=x-4,则函数的图象关于y轴对称;
当m=2时,y=x3m-7=y=x-1,则函数的图象关于原点对称;
所以m的值是1,
故选:C.
点评 本题考查幂函数的性质以及图象,属于基础题.

练习册系列答案
相关题目
20.运行下面的程序框图,输出的结果为( )
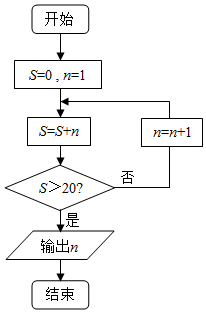

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
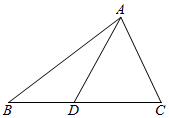 如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.
如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.