题目内容
5.若点M(3,1)、N(-1,3)均在直线ax-y+2=0的同一侧,则实数a的取值范围是( )| A. | $(-1,-\frac{1}{3})$ | B. | $(\frac{1}{3},1)$ | C. | $(-∞,-1)∪(-\frac{1}{3},+∞)$ | D. | $(-∞,\frac{1}{3})∪(1,+∞)$ |
分析 由题意可得(3a-1+2)(-a-3+2)>0,求解不等式得答案.
解答 解:∵点M(3,1)、N(-1,3)均在直线ax-y+2=0的同一侧,
∴(3a-1+2)(-a-3+2)>0,
解得:-1$<a<-\frac{1}{3}$.
故选:A.
点评 本题考查直线的斜率,考查了二元一次不等式表示的平面区域,是基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
15.已知$sin(x+\frac{π}{6})=\frac{1}{3}$,则$sin(x-\frac{5π}{6})+{sin^2}(\frac{π}{3}-x)$的值是$\frac{5}{9}$.
20.设集合A={x|-1<x≤2},B={x|0<x<2},则A∩B=( )
| A. | (-1,2] | B. | (0,2) | C. | (0,2] | D. | (1,+∞) |
10.已知方程(x2-mx+4)(x2-nx+4)=0的四个根组成一个首项$\frac{1}{4}$的等比数列,则|m-n|的值为( )
| A. | 0 | B. | $11\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
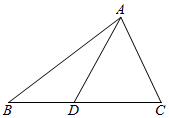 如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.
如图,在△ABC中,AB=12.AC=3$\sqrt{6}$,BC=5$\sqrt{6}$.点D在边BC上.且∠ADB=120°.