题目内容
已知抛物线Γ:x2=2my(m>0)和直线l:y=kx-m没有公共点(其中k,m为常数),动点P是直线l上的任意一点,过P点引抛物线Γ的两条切线,切点分别为M,N,且直线MN恒过点Q(k,1).
(1)求抛物线Γ的方程;
(2)已知O为坐标原点,连接PQ交抛物线Γ于A,B两点,且A点在线段PQ之间,求
•
+
•
的值.
(1)求抛物线Γ的方程;
(2)已知O为坐标原点,连接PQ交抛物线Γ于A,B两点,且A点在线段PQ之间,求
| PA |
| QB |
| PB |
| QA |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:压轴题,转化思想
分析:对第(1)问,先求二次函数y=
的导数,由点斜式得切线PM,PN的方程,由此得直线MN的方程,根据点P在l上及MN恒过点Q分别得方程,通过消参,最后可得m的值;
对第(2)问,可将向量的数量积转化为线段的长度,再转化为长度之比,从而利用相似三角形的相似比,以达到化简的目的.
| x2 |
| 2m |
对第(2)问,可将向量的数量积转化为线段的长度,再转化为长度之比,从而利用相似三角形的相似比,以达到化简的目的.
解答:
解:(Ⅰ)设M(x1,y1),N(x2,y2),P(x0,y0),
由x2=2my,得y=
,则y′=
,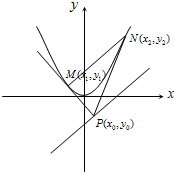
又
=2y1,
=2y2,
则切线PM的方程为y=
x-y1,切线PN的方程为y=
x-y2.
由于PM,PN经过点P,有
,
显然,M(x1,y1),N(x2,y2)的坐标满足方程y0=
x0-y,
根据两点确定一条直线,可知直线MN的方程就是y0=
x0-y,
∵MN恒过点(k,1),∴y0=
x0-1,
又点P在直线l上,有y0=kx0-1,联立上式消去kx0,得(y0+1)(m-1)=0,
由y0的任意性知,m=1,
∴抛物线Γ的方程为x2=2y.
(Ⅱ)由于P,A,B,Q四点共线,且A点在线段PQ之间,
可得
•
+
•
=|
|•|
|-|
|•|
|=|
||
|(
-
),
设A(x3,y3),B(x4,y4),根据相似三角形的对应边所成比例相等,
有
=
,
=
,
∴|
||
|(
-
)=|
||
|(
-
).
由P(x0,y0),Q(k,1),知直线PQ:y-1=
(x-k),
与抛物线方程x2=2y联立可得
x2-
x+
=0,
由韦达定理得x3+x4=
,…①
x3x4=
,…②
∴
-
=-
=-
,…③
将①、②式代入③式中得
-
=-
=-
.
将y0=kx0-1代入上式,得
-
=-
=0,
即
•
+
•
的值为0.
由x2=2my,得y=
| x2 |
| 2m |
| x |
| m |
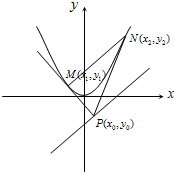
又
| ||
| m |
| ||
| m |
则切线PM的方程为y=
| x1 |
| m |
| x2 |
| m |
由于PM,PN经过点P,有
|
显然,M(x1,y1),N(x2,y2)的坐标满足方程y0=
| x |
| m |
根据两点确定一条直线,可知直线MN的方程就是y0=
| x |
| m |
∵MN恒过点(k,1),∴y0=
| k |
| m |
又点P在直线l上,有y0=kx0-1,联立上式消去kx0,得(y0+1)(m-1)=0,
由y0的任意性知,m=1,
∴抛物线Γ的方程为x2=2y.
(Ⅱ)由于P,A,B,Q四点共线,且A点在线段PQ之间,
可得
| PA |
| QB |
| PB |
| QA |
| PA |
| QB |
| PB |
| QA |
| PA |
| PB |
|
| ||
|
|
|
| ||
|
|
设A(x3,y3),B(x4,y4),根据相似三角形的对应边所成比例相等,
有
|
| ||
|
|
| x4-k |
| x4-x0 |
|
| ||
|
|
| k-x3 |
| x3-x0 |
∴|
| PA |
| PB |
|
| ||
|
|
|
| ||
|
|
| PA |
| PB |
| x4-k |
| x4-x0 |
| k-x3 |
| x3-x0 |
由P(x0,y0),Q(k,1),知直线PQ:y-1=
| y0-1 |
| x0-k |
与抛物线方程x2=2y联立可得
| 1 |
| 2 |
| y0-1 |
| x0-k |
| y0k-x0 |
| x0-k |
由韦达定理得x3+x4=
| 2(y0-1) |
| x0-k |
x3x4=
| 2y0k-2x0 |
| x0-k |
∴
| x4-k |
| x4-x0 |
| k-x3 |
| x3-x0 |
| (k-x4)(x3-x0)-(x3-k)(x4-x0) |
| (x4-x0)(x3-x0) |
| (x3+x4)(k+x0)-2x3x4-2kx0 |
| (x4-x0)(x3-x0) |
将①、②式代入③式中得
| x4-k |
| x4-x0 |
| k-x3 |
| x3-x0 |
| ||||
| (x4-x0)(x3-x0) |
=-
2x0y0-2k+2x0-2y0k-2k
| ||
| (x0-k)(x4-x0)(x3-x0) |
将y0=kx0-1代入上式,得
| x4-k |
| x4-x0 |
| k-x3 |
| x3-x0 |
2x0(kx0-1)-2k+2x0-2k(kx0-1)-2k
| ||
| (x0-k)(x4-x0)(x3-x0) |
即
| PA |
| QB |
| PB |
| QA |
点评:1.本题难度较大,涉及的参数较多,如何消参成了解决本题的主要任务,常用方法是代入法.
2.求
•
+
•
时,若根据向量向量积的坐标进行运算,则计算量太大,很难算出结果,本题先将数量积转化为长度,再将长度转化为横坐标的计算,计算量明显减少.
3.本题涉及直线与圆锥曲线相交的问题,联立直线与曲线的方程,消去y,得到一个关于x的一元二次方程,利用韦达定理消元,体现了“设而不求”的思想.
2.求
| PA |
| QB |
| PB |
| QA |
3.本题涉及直线与圆锥曲线相交的问题,联立直线与曲线的方程,消去y,得到一个关于x的一元二次方程,利用韦达定理消元,体现了“设而不求”的思想.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
三个数a,b,c既是等差数列,又是等比数列,则a,b,c间的关系为( )
| A、b-a=c-b | ||||||
| B、b2=ac | ||||||
| C、a=b=c | ||||||
D、
|
已知数列{an}中,a3=2,a5=1,若{
}是等差数列,则a11等于( )
| 1 |
| 1+an |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
在△ABC中,若c=acosB,则△ABC中一定为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |