题目内容
已知a,b∈R,若a>b,则下列不等式成立的是( )
| A、lga>lgb | ||||||
| B、0.5a>0.5b | ||||||
C、a
| ||||||
D、
|
考点:不等式比较大小
专题:不等式的解法及应用
分析:A.通过a,b取特殊值,即可得出选项的正误;
B.由a>b,利用指数函数的单调性即可得出,不正确;
C.通过a,b取特殊值,即可得出选项的正误;
D.利用函数f(x)=
在R上单调递增即可得出,正确.
B.由a>b,利用指数函数的单调性即可得出,不正确;
C.通过a,b取特殊值,即可得出选项的正误;
D.利用函数f(x)=
| 3 | x |
解答:
解:对于A.取a=-1,b=-2,无意义,不正确;
对于B.∵a>b,∴0.5a<0.5b,不正确;
对于C.取a=-1,b=-2,无意义,不正确;
对于D.由于函数f(x)=
在R上单调递增,又a>b,因此
>
,正确.
故选:D.
对于B.∵a>b,∴0.5a<0.5b,不正确;
对于C.取a=-1,b=-2,无意义,不正确;
对于D.由于函数f(x)=
| 3 | x |
| 3 | a |
| 3 | b |
故选:D.
点评:本题考查了指数函数、对数函数与幂函数的单调性,不等式的性质,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
若实数x,y满足
,则|x|+y的取值范围为( )
|
| A、[2,3] |
| B、[0,3] |
| C、[-1,2] |
| D、[-1,3] |
f(x)是定义在D上的函数,若存在区间,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x)是k型函数.若函数y=-
x2+x[m,n]⊆D是3型函数,则m+n的值为( )
| 1 |
| 2 |
| A、0 | B、8 | C、-4 | D、-4或8 |
已知函数f(x)=
,若对任意xx≠x2,都有
<0成立,则a的取值范围是( )
|
| f(x1)-f(x ) |
| x1-x2 |
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(-1,2) |
已知α,β均为锐角,cos(α+β)=-
,cosα=
,则角cosβ为( )
| 11 |
| 14 |
| 1 |
| 7 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
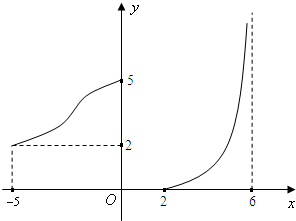 函数y=f(x)的图象如图所示,根据图象回答下列问题:
函数y=f(x)的图象如图所示,根据图象回答下列问题: