Question

11．方程log₃x+x-3=0的解所在区间是（k，k+1）（k∈Z），则k=2．

Answer 1

分析 方程的解所在的区间，则对应的函数的零点在这个范围，把原函数写出两个初等函数，即两个初等函数的交点在这个区间，结合两个函数的草图得到函数的交点的位置在（2，3），再进行进一步检验．

解答 解：∵方程log₃x+x=3即log₃x=-x+3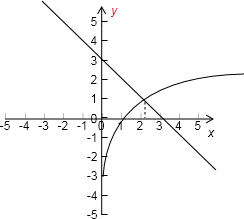
根据两个基本函数的图象可知两个函数的交点一定在（1，3），
因m（x）=log₃x+x-3在（2，3）上不满足m（3）m（2）＜0，
方程 log₃x+x-3=0 的解所在的区间是（2，3），
∴k=2，
故答案为2．

点评 本题考查函数零点的检验，考查函数与对应的方程之间的关系，是一个比较典型的函数的零点的问题，注意解题过程中数形结合思想的应用．