题目内容
7．命题“?x∈R，sinx+cosx≤$\sqrt{2}$”的否定是（ ）| A． | ?x∈R，sinx+cosx＞$\sqrt{2}$ | B． | ?x∈R，sinx+cosx≤$\sqrt{2}$ | ||
| C． | ?x∈R，sinx+cosx≥$\sqrt{2}$ | D． | ?x∈R，sinx+cosx＞$\sqrt{2}$ |
分析 由带量词的命题否定规则可得．
解答 解：∵命题“?x∈R，sinx+cosx≤$\sqrt{2}$”是一个全称命题，
又∵全称命题的否定是特称命题，
∴原命题的否定为“?∈R，sinx+cosx＞$\sqrt{2}$”
故选：D
点评 本题考查全称命题的否定，属基础题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
18．从统计学的角度看，下列关于变量间的关系说法正确的是（ ）
| A． | 人体的脂肪含量与年龄之间没有相关关系 | |
| B． | 汽车的重量和汽车每消耗1L汽油所行驶的平均路程负相关 | |
| C． | 吸烟量与健康水平正相关 | |
| D． | 气温与热饮销售好不好正相关 |
15．如图所示，角θ的终边与单位圆交于点P（-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{6}}{3}$），则cos（π-θ）的值为（ ）
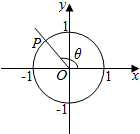
| A． | -$\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | -$\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
2．已知A（-1，1），B（3，1），C（1，3），则△ABC的BC边上的高所在的直线的方程为（ ）
| A． | x+y+2=0 | B． | x+y=0 | C． | x-y+2=0 | D． | x-y=0 |
12．
如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD是直角梯形，∠BAD=∠ADC=90°，E为CB的中点，AB=PA=AD=2CD，则PA与平面PDE所成的角的正弦值为（ ）
如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD是直角梯形，∠BAD=∠ADC=90°，E为CB的中点，AB=PA=AD=2CD，则PA与平面PDE所成的角的正弦值为（ ）| A． | $\frac{\sqrt{22}}{22}$ | B． | $\frac{\sqrt{22}}{11}$ | C． | $\frac{3\sqrt{22}}{22}$ | D． | $\frac{2\sqrt{22}}{11}$ |
16．在等差数列{an}中，a5=5，a10=15，则a15=（ ）
| A． | 20 | B． | 25 | C． | 45 | D． | 75 |
17．下列说法正确的是（ ）
| A． | 动物和植物的机体都是细胞组成的；植物细胞中有细胞核，所以动物细胞中也有细胞核．此推理是归纳推理 | |
| B． | “由圆的性质推出球的有关性质”是类比推理 | |
| C． | 观察下列各式：a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…则可得到a10+b10=122 | |
| D． | 函数f（x）是可导函数，已知f′（a）=0则a为f（x）的极值点 |