题目内容
19.已知直线l过点(1,4).(1)若直线l与直线l1:y=2x平行,求直线l的方程并求l与l1间的距离;
(2)若直线l在x轴与y轴上的截距均为a,且a≠0,求a的值.
分析 (1)由于直线l过点(1,4)与直线l1:y=2x平行,则y-4=2(x-1),再利用相互平行的直线斜率之间的距离公式即可得出;
(2)由题意可得直线l的方程为:$\frac{x}{a}+\frac{y}{a}$=1,把点(1,4)代入解得a即可得出.
解答 解:(1)由于直线l过点(1,4)与直线l1:y=2x平行,则y-4=2(x-1),化为y=2x+2.
l与l1间的距离d=$\frac{|2-0|}{\sqrt{{2}^{2}+(-1)^{2}}}$=$\frac{2\sqrt{5}}{5}$.
(2)由题意可得直线l的方程为:$\frac{x}{a}+\frac{y}{a}$=1,把点(1,4)代入可得:$\frac{1}{a}+\frac{4}{a}$=1,解得a=5.
点评 本题考查了相互平行的直线斜率之间的关系及其距离、截距式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
7.命题“?x∈R,sinx+cosx≤$\sqrt{2}$”的否定是( )
| A. | ?x∈R,sinx+cosx>$\sqrt{2}$ | B. | ?x∈R,sinx+cosx≤$\sqrt{2}$ | ||
| C. | ?x∈R,sinx+cosx≥$\sqrt{2}$ | D. | ?x∈R,sinx+cosx>$\sqrt{2}$ |
14.已知集合A={1,2,3},B={x|(x-3)(x-6)=0},则A∩B等于( )
| A. | {1} | B. | {2,3} | C. | {3,6} | D. | {3} |
8.已知命题p:“?x∈R,x+1≥0”的否定是“?x∈R,x+1<0”;命题q:函数y=x-3是幂函数,则下列命题为真命题的是( )
| A. | p且q | B. | p或q | C. | ¬q | D. | p且(¬q) |
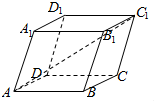 已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.
已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.