题目内容
15.如图所示,角θ的终边与单位圆交于点P(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$),则cos(π-θ)的值为( )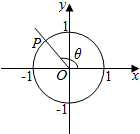
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 由条件利用任意角的三角函数的定义求得cosθ的值,再利用诱导公式求得cos(π-θ)的值.
解答 解:∵角θ的终边与单位圆交于点P(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$),∴x=-$\frac{\sqrt{3}}{3}$,y=$\frac{\sqrt{6}}{3}$,r=|OP|=$\sqrt{{x}^{2}{+y}^{2}}$=1,
则cos(π-θ)=-cosθ=-$\frac{x}{r}$=$\frac{\sqrt{3}}{3}$,
故选:B.
点评 本题主要考查任意角的三角函数的定义,诱导公式的应用,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
6.定义域为R的偶函数f(x)满足:对任意x∈R都有f(2-x)=f(x),且当x∈[0,1]时,f(x)=x-1,若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则a的取值范围为( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,1) |
7.命题“?x∈R,sinx+cosx≤$\sqrt{2}$”的否定是( )
| A. | ?x∈R,sinx+cosx>$\sqrt{2}$ | B. | ?x∈R,sinx+cosx≤$\sqrt{2}$ | ||
| C. | ?x∈R,sinx+cosx≥$\sqrt{2}$ | D. | ?x∈R,sinx+cosx>$\sqrt{2}$ |
 为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况编成如图所示的茎叶图(单位:个):若挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.
为了解某地脐橙种植情况,调研小组在该地某脐橙种植园中随机抽出30棵,每棵挂果情况编成如图所示的茎叶图(单位:个):若挂果在175个以上(包括175)定义为“高产”,挂果在175个以下(不包括175)定义为“非高产”.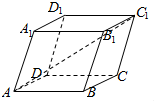 已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.
已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$. 如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.
如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.