Question

某海轮以30n mile/h的速度航行，在A点测得海面上油井P在南偏东60°方向，向北航行40min后到达B点，测得油井P在南偏东30°方向，海轮改为北偏东60°的航向再行驶80min到达C点，求P、C间的距离．

Answer 1

考点：解三角形的实际应用

专题：应用题,解三角形

分析：在△ABP中，根据正弦定理，求BP，再利用余弦定理算出PC的长，即可算出P、C两地间的距离．

解答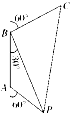： 解：如图，在△ABP中，AB=30×

40

60

=20，∠APB=30°，∠BAP=120°，
根据正弦定理，

AB

sin∠BPA

=

BP

sin∠BAP

　得：

20

1 2

=

BP

3 2

，∴BP=20

3

．
在△BPC中，BC=30×

80

60

=40．
由已知∠PBC=90°，∴PC=

PB2+BC2

=20

7

（n mile）      
答：P、C间的距离为20

7

 n mile．

点评：本题给出实际应用问题，求两地之间的距离，着重考查了正弦定理、余弦定理和解三角形的实际应用等知识，属于中档题．