题目内容
12.已知函数f(x)=2cosx(sinx+cosx),x∈R.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)求函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上的最小值和最大值.
分析 ( I)化函数f(x)为正弦型函数,求出f(x)的最小正周期;
(Ⅱ)根据正弦函数的单调性求出f(x)的单调增区间;
(III)根据x的取值范围求出2x+$\frac{π}{4}$的取值范围,从而求出f(x)的最值.
解答 解:( I)函数f(x)=2cosx(sinx+cosx)
=2sinxcosx+2cos2x
=sin2x+cos2x+1
=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+1,
∴函数f(x)的最小正周期为:
T=$\frac{2π}{ω}$=π;
(Ⅱ) 由$2kπ-\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$,
解得$kπ-\frac{3π}{8}≤x≤kπ+\frac{π}{8}$,
∴函数f(x)的单调递增区间为
$[kπ-\frac{3π}{8},kπ+\frac{π}{8}]$(k∈Z);
( III)由 $-\frac{π}{4}≤x≤\frac{π}{4}$,
得 $-\frac{π}{4}≤2x+\frac{π}{4}≤\frac{3π}{4}$,
令2x+$\frac{π}{4}$=-$\frac{π}{4}$,解得x=-$\frac{π}{4}$,
∴f(x)min=$f(-\frac{π}{4})$=$\sqrt{2}$×(-$\frac{\sqrt{2}}{2}$)+1=0,
令2x+$\frac{π}{4}$=$\frac{π}{2}$,解得x=$\frac{π}{8}$,
∴f(x)max=$f(\frac{π}{8})$=$\sqrt{2}$×1+1=$\sqrt{2}$+1.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角恒等变换问题,是基础题目.

练习册系列答案
相关题目
3.不等式x2-4x+3<0的解集为( )
| A. | (1,3) | B. | (-3,-1) | C. | (-∞,-3)∪(-1,+∞) | D. | (-∞,1)∪(3,+∞) |
20.为了得到函数$y=cos(2x-\frac{π}{2})$的图象,可以将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向左平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
7.函数f(x)=3x+2x-3的零点所在的区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
3.设f(x)=$\left\{\begin{array}{l}{(x-a)^2},x≤0\\ x+\frac{1}{x}+a+4,x>0\end{array}$,若f(0)是f(x)的最小值,则a的取值范围为( )
| A. | [-2,3] | B. | [-2,0] | C. | [1,3] | D. | [0,3] |
19.执行如图所示的程序框图,输出S的值为( )
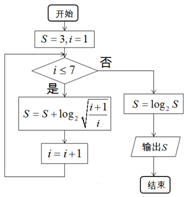

| A. | log210-1 | B. | 2log23-1 | C. | $\frac{9}{2}$ | D. | 6 |
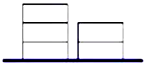 如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).
如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).