题目内容
16.已知双曲线$\frac{x^2}{4}-\frac{y^2}{b^2}=1(b>0)$,以原点为圆心,双曲线的实半轴为半径长的圆与双曲线的两条渐近线相交于A.B.C.D.四点,四边形ABCD的面积为2b,则双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1.分析 以原点为圆心,双曲线的实半轴长为半径长的圆的方程为x2+y2=4,双曲线的两条渐近线方程为y=±$\frac{b}{2}$x,利用四边形ABCD的面积为2b,求出A的坐标,代入圆的方程,即可得出结论.
解答 解:以原点为圆心,双曲线的实半轴长为半径长的圆的方程为x2+y2=4,
双曲线的两条渐近线方程为y=±$\frac{b}{2}$x,
设A(x,$\frac{b}{2}$x),∵四边形ABCD即矩形ABCD的面积为2b,
∴2x•bx=2b,
∴x=±1,
将A(1,$\frac{b}{2}$)代入x2+y2=4,可得1+$\frac{{b}^{2}}{4}$=4,∴b2=12,
∴双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1,
故答案为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1.
点评 本题考查双曲线的方程与性质,注意运用方程思想和代入法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
8.p:?x0∈R,x${\;}_{0}^{2}$+m≤0,q:?x∈R,x2+mx+1>0,如果p,q都是命题且(¬p)∨q为假命题,则实数m的取值范围是( )
| A. | m≤-2 | B. | -2≤m≤0 | C. | 0≤m≤2 | D. | m≥2 |
5.函数y=log2(x+2)的定义域是( )
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-2,+∞) | D. | [-2,+∞) |
1.已知函数f(x)=Asin(ωx+φ)$(A>0,|φ|<\frac{π}{2})$的图象(部分)如图所示,则$f(-\frac{1}{2})$=( )
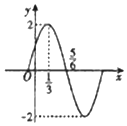

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
5.设偶函数f(x)满足f(x)=2x-4(x≥0),则满足f(a-2)>0的实数a的取值范围为( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |