题目内容
4．若点（5，b）在两条平行直线$3x-4y+\frac{1}{2}=0$与6x+8y+10=0之间，则整数b的值为（ ）| A． | 5 | B． | -5 | C． | 4 | D． | -4 |
分析 由题意，（15-4b+$\frac{1}{2}$）（30-8b+10）＜0，即可求出整数b的值．
解答 解：由题意，（15-4b+$\frac{1}{2}$）（30-8b+10）＜0，
∴$\frac{31}{8}$＜b＜5，
∴整数b的值为4，
故选C．
点评 本题考查不等式的解法，考查平行线，考查学生分析解决问题的能力，比较基础．
练习册系列答案
备战中考寒假系列答案
相关题目
12．函数$y=sin（-\frac{x}{2}-\frac{π}{6}）$的单调递增区间是（ ）
| A． | [2kπ+$\frac{2}{3}$π，2kπ+$\frac{8}{3}$π]（k∈Z） | B． | [4kπ+$\frac{2}{3}$π，4kπ+$\frac{8}{3}$π]（k∈Z） | ||
| C． | [2kπ-$\frac{4}{3}$π，2kπ+$\frac{2}{3}$π]（k∈Z） | D． | [4kπ-$\frac{4}{3}$π，4kπ+$\frac{2}{3}$π]（k∈Z） |
19．
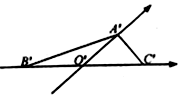已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图，其中 B'O'=C'O'=1，${A}'{O}'=\frac{{\sqrt{3}}}{2}$，那么对于原△ABC则有（ ）
已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图，其中 B'O'=C'O'=1，${A}'{O}'=\frac{{\sqrt{3}}}{2}$，那么对于原△ABC则有（ ）| A． | AB=BC | B． | AB=BC，且AB⊥BC | C． | AB⊥BC | D． | AB=AC，且AB⊥AC |