题目内容
10.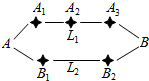 “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.(1)若走L1路线,求最多遇到1次堵塞的概率;
(2)若走L2路线,路上遇到的堵塞次数为X,求随机变量X的分布列与数学期望.
分析 (1)设走l1路线最多遇到1次堵塞为A事件,利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出走L1路线,最多遇到1次堵塞的概率.
(2)依题意X的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
解答 解:(1)设走l1路线最多遇到1次堵塞为A事件,
则P(A)=${C}_{3}^{0}(\frac{1}{3})^{3}$+${C}_{3}^{1}×\frac{2}{3}×(\frac{1}{3})^{2}$=$\frac{7}{27}$,
∴走L1路线,最多遇到1次堵塞的概率为$\frac{7}{27}$.
(2)依题意X的可能取值为0,1,2,
P(X=0)=$(1-\frac{3}{4})(1-\frac{3}{5})$=$\frac{1}{10}$,
P(X=1)=$\frac{3}{4}×(1-\frac{3}{5})+(1-\frac{3}{4})×\frac{3}{5}$=$\frac{9}{20}$,
P(X=2)=$\frac{3}{4}×\frac{3}{5}$=$\frac{9}{20}$,
∴随机变量X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{9}{20}$ | $\frac{9}{20}$ |
点评 本题考查概率的求法,考查离散型随机变量分布列、数学期望的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
5.函数f(x)=lgx-$\frac{9}{x}$的零点所在的区间是( )
| A. | (10,100) | B. | ($\sqrt{10}$,10) | C. | (1,$\sqrt{10}$) | D. | (0,1) |
15.若f(x)=$\left\{\begin{array}{l}{lgx,}&{x>0}\\{x+{∫}_{0}^{a}3{t}^{2}dt,}&{x≤0}\end{array}\right.$,f(f(1))=1,则a的值是( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
2.已知直线l与直线2x-3y+4=0关于直线x=1对称,则直线l的方程为( )
| A. | 2x+3y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
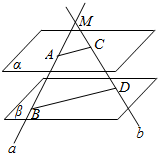 如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.
如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.