题目内容
20．曲线y=$\frac{1}{2}$x2-2x在点（1，-$\frac{3}{2}$）处切线的倾斜角为$\frac{3π}{4}$．分析 求出函数的导数，求得切线的斜率，由直线的斜率公式k=tanθ，计算即可得到所求值．
解答 解：y=$\frac{1}{2}$x2-2x的导数为y′=x-2，
由导数的几何意义可得，
在点（1，-$\frac{3}{2}$）处切线的斜率为k=-1，
即有tanθ=-1，（θ∈[0，π）），
可得θ=$\frac{3π}{4}$．
故答案为：$\frac{3π}{4}$．
点评 本题考查导数的运用：求切线的斜率，考查导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，考查直线的斜率公式的运用，属于基础题．
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
10．2015年9月3日，抗战胜利70周年纪念活动在北京隆重举行，受到全国人民的瞩目．纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等，据统计，抗战老兵由于身体原因，参加纪念大会、阅兵式、招待会这三个环节（可参加多个，也可都不参加）的情况及其概率如表所示：
（Ⅰ）若m=2n，则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈，求参加纪念活动环节数为2的抗战老兵中抽取的人数；
（Ⅱ）某医疗部门决定从（1）中抽取的6名抗战老兵中随机抽取2名进行体检，求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率．
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
（Ⅱ）某医疗部门决定从（1）中抽取的6名抗战老兵中随机抽取2名进行体检，求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率．
11．一个圆内有一个内接等边三角形，一动点在圆内运动，则此点落在等边三角形内部的概率为（ ）
| A． | $\frac{3}{π}$ | B． | $\frac{{3\sqrt{3}}}{4π}$ | C． | $\frac{{\sqrt{3}}}{4π}$ | D． | $\frac{{2\sqrt{3}}}{3π}$ |
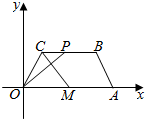在平面直角坐标系xOy中，已知四边形OABC是等腰梯形，OA∥BC，$A（6，0），C（1，\sqrt{3}）$，点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$，点P在线段BC上运动（包括端点），如图．
5．同时抛掷两枚骰子，向上点数之和为5的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{21}$ | C． | $\frac{1}{18}$ | D． | $\frac{1}{6}$ |
某单位有40名职工，现从中抽取5名职工，统计他们的体重，获得体重数据的茎叶图如图所示，则该样本的标准差为$\sqrt{62}$．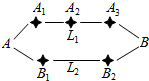
“十一黄金周”期间某市再次迎来了客流高峰，小李从该市的A地到B地有L1、L2两条路线（如图），L1路线上有A1、A2、A3三个路口，各路口遇到堵塞的概率均为$\frac{2}{3}$；L2路线上有B1、B2两个路口，各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$．