题目内容
18．袋中有形状、大小都相同的5只球，其中1只白球，2只红球，2只黄球，从中一次随机摸出2只球，则这2只球颜色不同的概率为$\frac{4}{5}$．分析 这2只球颜色不同的对立事件是两只球颜色不同，由此能求出这2只球颜色不同的概率．
解答 解：袋中有形状、大小都相同的5只球，其中1只白球，2只红球，2只黄球，
从中一次随机摸出2只球，基本事件总数n=${C}_{5}^{2}$=10，
这2只球颜色不同的对立事件是两只球颜色不同，
∴这2只球颜色不同的概率：
p=1-$\frac{{C}_{2}^{2}+{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{4}{5}$．
故答案为：$\frac{4}{5}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
练习册系列答案
相关题目
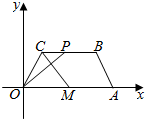在平面直角坐标系xOy中，已知四边形OABC是等腰梯形，OA∥BC，$A（6，0），C（1，\sqrt{3}）$，点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$，点P在线段BC上运动（包括端点），如图．
某单位有40名职工，现从中抽取5名职工，统计他们的体重，获得体重数据的茎叶图如图所示，则该样本的标准差为$\sqrt{62}$．
6．函数f（x）=x3的图象经过（ ）
| A． | 第一、三象限 | B． | 第二、三象限 | C． | 第一、二象限 | D． | 第一、四象限 |
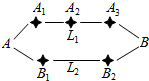“十一黄金周”期间某市再次迎来了客流高峰，小李从该市的A地到B地有L1、L2两条路线（如图），L1路线上有A1、A2、A3三个路口，各路口遇到堵塞的概率均为$\frac{2}{3}$；L2路线上有B1、B2两个路口，各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$．
8．方程y一1=$\sqrt{1-{x}^{2}}$表示的曲线是（ ）
| A． | 直线 | B． | 射线 | C． | 圆 | D． | 半圆 |