题目内容
2.已知直线l与直线2x-3y+4=0关于直线x=1对称,则直线l的方程为( )| A. | 2x+3y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
分析 设P(x,y)为直线l上的任意一点,则点P关于直线x=1的对称点为P′(2-x,y),代入直线2x-3y+4=0即可得出.
解答 解:设P(x,y)为直线l上的任意一点,则点P关于直线x=1的对称点为P′(2-x,y),
代入直线2x-3y+4=0可得:2(2-x)-3y+4=0,化为2x+3y-8=0,
故选:A.
点评 本题考查了轴对称性质、直线方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过点F2且斜率为$\frac{2b}{a}$的直线l交直线2bx+ay=0于M,若M在以线段F1F2为直径的圆上,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
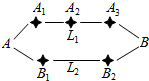 “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.