题目内容
样本(x1,x2,…,xn)的平均数为x,样本(y1,y2,…,yn)的平均数为y(y≠x),样本(x1,x2,…,xn,y1,y2,…,yn)的平均数z=λx+μy,若直线l:(λ+2)x-(1+2μ)y+1-3λ=0,则下列叙述不正确的有
①直线l恒过定点(1,1);
②直线l与圆 (x-1)2+(y-1)2=4相交;
③直线l到原点的最大距离为
;
④直线l与直线l′:(2λ-3)x-(3-μ)y=0垂直.( )
①直线l恒过定点(1,1);
②直线l与圆 (x-1)2+(y-1)2=4相交;
③直线l到原点的最大距离为
| 2 |
④直线l与直线l′:(2λ-3)x-(3-μ)y=0垂直.( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:先确定λ=μ=0.5,再对选项进行判断即可.
解答:
解:∵样本(x1,x2,…,xn)的平均数为x,样本(y1,y2,…,yn)的平均数为y(y≠x),样本(x1,x2,…,xn,y1,y2,…,yn)的平均数z=λx+μy,
∴λ=μ=0.5,
∴直线l:(λ+2)x-(1+2μ)y+1-3λ=0为5x-4y-1=0,
①直线l恒过定点(1,1),正确;
②圆心在直线l上,∴直线l与圆(x-1)2+(y-1)2=4相交,故正确;
③直线l到原点的最大距离为圆心到原点的距离
,故正确;
④直直线l′:(2λ-3)x-(3-μ)y=0为4x+5y=0,∴直线l与直线l′:(2λ-3)x-(3-μ)y=0垂直,正确.
故选:A.
∴λ=μ=0.5,
∴直线l:(λ+2)x-(1+2μ)y+1-3λ=0为5x-4y-1=0,
①直线l恒过定点(1,1),正确;
②圆心在直线l上,∴直线l与圆(x-1)2+(y-1)2=4相交,故正确;
③直线l到原点的最大距离为圆心到原点的距离
| 2 |
④直直线l′:(2λ-3)x-(3-μ)y=0为4x+5y=0,∴直线l与直线l′:(2λ-3)x-(3-μ)y=0垂直,正确.
故选:A.
点评:本题考查直线和圆的方程的应用,考查统计知识,确定λ=μ=0.5是关键.

练习册系列答案
相关题目
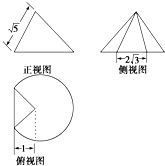 一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
经过圆x2+(y+1)2=1的圆心C,且与直线2x+3y-4=0平行的直线方程为( )
| A、2x+3y+3=0 |
| B、2x+3y-3=0 |
| C、2x+3y+2=0 |
| D、3x-2y-2=0 |
△ABC中,∠C=120°,a,b是方程x2-3x+2=0的两根,则c的值为( )
| A、3 | ||
| B、7 | ||
C、
| ||
D、
|
若m>0且m≠1,n>0,则“logmn>0”是“(m-1)(n-1)>0”的( )条件.
| A、充要 |
| B、充分不必要 |
| C、必要不充分 |
| D、既不充分也不必要 |
已知函数f(x)=
x3+ax2-4在区间(0,2)上是减函数,则a的范围是( )
| 1 |
| 3 |
| A、(-∞,3] |
| B、[-1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1] |