题目内容
已知双曲线
-
=1(m>0,n>0)的离心率为2,有一个焦点与抛物线y2=16x的焦点重合,则mn的值为 .
| x2 |
| m |
| y2 |
| n |
考点:双曲线的简单性质,抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据抛物线方程求得抛物线的焦点,进而可知双曲线的焦距,根据双曲线的离心率求得m,最后根据m+n=16,求得n,则答案可得.
解答:
解:∵抛物线y2=16x的焦点为(4,0),则双曲线的焦距为8,
则有m+n=16,①
∵双曲线
-
=1(m>0,n>0)的离心率为2,
∴e=
=
=2②
由①②解得m=4,n=12,
∴mn=48
故答案为:48.
则有m+n=16,①
∵双曲线
| x2 |
| m |
| y2 |
| n |
∴e=
| c |
| a |
| 4 | ||
|
由①②解得m=4,n=12,
∴mn=48
故答案为:48.
点评:本题主要考查了圆锥曲线的共同特征.解题的关键是对圆锥曲线的基本性质熟练掌握,属于基础题.

练习册系列答案
相关题目

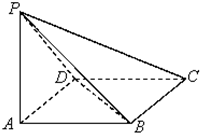 如图,已知四棱锥P-ABCD,侧棱PA⊥平面ABCD,底面ABCD为菱形,∠DAB=60°且PA=AB,则直线AB与平面PBC所成角的正弦值为
如图,已知四棱锥P-ABCD,侧棱PA⊥平面ABCD,底面ABCD为菱形,∠DAB=60°且PA=AB,则直线AB与平面PBC所成角的正弦值为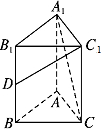 如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为