题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p或q”是假命题,求实数a的取值范围.
解:由a2x2+ax-2=0,得
(ax+2)(ax-1)=0,
显然a≠0,∴ x=- 或x=
或x= .
.
∵ x∈[-1,1],故 ≤1或
≤1或 ≤1,
≤1,
∴ |a|≥1.
由题知命题q“只有一个实数x满足x2+2ax+2a≤0”,
即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴ Δ=4a2-8a=0,∴ a=0或a=2,
∴ 当命题“p或q”为真命题时|a|≥1或a=0.
∵ 命题“p或q”为假命题,
∴ a的取值范围为{a|-1<a<0或0<a<1}.

练习册系列答案
相关题目
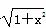 ),是奇函数,p2:函数y=x
),是奇函数,p2:函数y=x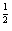 为偶函数,则下列四个命题:
为偶函数,则下列四个命题: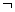 p1)∨p2;④ p1∧(
p1)∨p2;④ p1∧(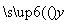 =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且 =1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是________.
=1渐近线上的一个动点P总在平面区域(x-m)2+y2≥16内,则实数m的取值范围是________.