题目内容
已知复数z满足|z+1|=|z-1|,且z+
∈R.
(1)求复数z;
(2)请写出一个以z为根的实系数一元二次方程.
| 1 |
| z |
(1)求复数z;
(2)请写出一个以z为根的实系数一元二次方程.
考点:复数代数形式的混合运算,复数代数形式的乘除运算
专题:坐标系和参数方程
分析:(1)设z=a+bi(a,b∈R),利用复数的运算法则、模的计算公式、复数为实数的充要条件即可得出;
(2)x2+1=0,满足条件.
(2)x2+1=0,满足条件.
解答:
解:(1)设z=a+bi(a,b∈R),∵复数z满足|z+1|=|z-1|,且z+
∈R.
∴
=
,a+bi+
=a+bi+
,即
=0,
联立解得a=0,b=±1.
∴z=±i.
(2)x2+1=0,其根为:x=±i.
| 1 |
| z |
∴
| (a+1)2+b2 |
| (a-1)2+b2 |
| 1 |
| a+bi |
| a-bi |
| a2+b2 |
| b(a2+b2)-b |
| a2+b2 |
联立解得a=0,b=±1.
∴z=±i.
(2)x2+1=0,其根为:x=±i.
点评:本题考查了复数的运算法则、模的计算公式、复数为实数的充要条件,考查了计算能力,属于基础题.

练习册系列答案
相关题目
 写出下列关于角的集合.
写出下列关于角的集合.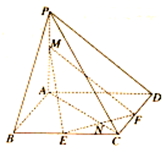 如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA
如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA