题目内容
计算下列定积分
sin2
dx.
| ∫ |
0 |
| x |
| 2 |
考点:定积分
专题:导数的概念及应用
分析:先根据二倍角公式,被积函数化为
(1-cosx),再根据定积分的计算法则计算即可.
| 1 |
| 2 |
解答:
解:
sin2
dx=
(1-cosx)dx=
(x-sinx)|
=
(
-1)=
-
.
| ∫ |
0 |
| x |
| 2 |
| ∫ |
0 |
| 1 |
| 2 |
| 1 |
| 2 |
0 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
点评:本题考查了三角形函数的化简以及定积分的计算,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
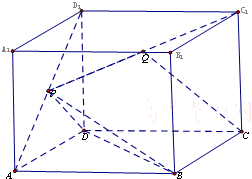 如图,在正方体ABCD-A1B1C1D1中,P为线段AD1上的中点,Q为线段PC1上的中点.
如图,在正方体ABCD-A1B1C1D1中,P为线段AD1上的中点,Q为线段PC1上的中点.