题目内容
在△ABC中,若sin(2π-A)=-
sin(π-B),
cosA=-
cos(π-B),则∠C= .
| 2 |
| 3 |
| 2 |
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:已知两式利用诱导公式化简,再利用同角三角函数间的基本关系变形求出cosA的值,进而求出A的度数,代入求出cosB的值,确定出B的度数,即可求出C的度数.
解答:
解:∵在△ABC中,sin(2π-A)=-
(π-B),
cosA=-
cos(π-B),
∴-sinA=-
sinB,即sinA=
sinB①,
cosA=
cosB②,
①2+②2得:sin2A+3cos2A=2,即1+2cos2A=2,
整理得:cos2A=
,即cosA=±
,
∴A=
或
,
当A=
时,由②得:
×
=
cosB,即cosB=
,
∴B=
,C=
;
当A=
时,由②得:
×(-
)=
cosB,即cosB=-
(不合题意,舍去),
综上,C=
.
故答案为:
.
| 2 |
| 3 |
| 2 |
∴-sinA=-
| 2 |
| 2 |
| 3 |
| 2 |
①2+②2得:sin2A+3cos2A=2,即1+2cos2A=2,
整理得:cos2A=
| 1 |
| 2 |
| ||
| 2 |
∴A=
| π |
| 4 |
| 3π |
| 4 |
当A=
| π |
| 4 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 2 |
∴B=
| π |
| 6 |
| 7π |
| 12 |
当A=
| 3π |
| 4 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 2 |
综上,C=
| 7π |
| 12 |
故答案为:
| 7π |
| 12 |
点评:此题考查了同角三角函数间的基本关系,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
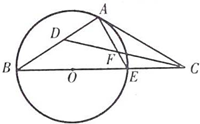 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点.F
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点.F