题目内容
 如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA
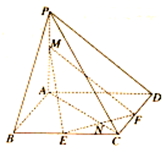
如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA上一动点,E,F分别是线段BC、CD的中点,EF与AC交于点N.
(1)求证:平面PAC⊥平面MEF;
(2)若PC∥平面MEF,试求PM:MA的值.
考点:直线与平面平行的判定,平面与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由已知可证明PA⊥EF,由底面ABCD为正方形,E,F分别是线段BC、CD的中点,EF与AC交于点N,可证明AC⊥EF,从而可得EF⊥平面PAC,又EF?平面MEF,即可判定平面PAC⊥平面MEF;
(2)连接MN,由PC∥平面MEF,且MN?平面MEF,MN?平面APC,可得PC∥MN,从而有
=
,设BC=2,则可得EC=1,AC=
,EN=
,CN=
,从而可求PM:MA的值.
(2)连接MN,由PC∥平面MEF,且MN?平面MEF,MN?平面APC,可得PC∥MN,从而有
| PM |
| MA |
| CN |
| NA |
| 8 |
| ||
| 2 |
| ||
| 2 |
解答:
 解:(1)∵PA⊥底面ABCD,∴PA⊥EF,
解:(1)∵PA⊥底面ABCD,∴PA⊥EF,
∵底面ABCD为正方形,E,F分别是线段BC、CD的中点,EF与AC交于点N.
∴∠ACB=
,设BC=2,可得EC=1,EN=
,可解得AC⊥EF,
∴EF⊥平面PAC,
∵EF?平面MEF,
∴平面PAC⊥平面MEF;
(2)连接MN,∵PC∥平面MEF,且MN?平面MEF,MN?平面APC,
∴PC∥MN,
∴
=
,
∵由(1)可得设BC=2,则EC=1,AC=
,EN=
,故CN=
=
,
∴解得:
=
=
=
.
 解:(1)∵PA⊥底面ABCD,∴PA⊥EF,
解:(1)∵PA⊥底面ABCD,∴PA⊥EF,∵底面ABCD为正方形,E,F分别是线段BC、CD的中点,EF与AC交于点N.
∴∠ACB=
| π |
| 4 |
| ||
| 2 |
∴EF⊥平面PAC,
∵EF?平面MEF,
∴平面PAC⊥平面MEF;
(2)连接MN,∵PC∥平面MEF,且MN?平面MEF,MN?平面APC,
∴PC∥MN,
∴
| PM |
| MA |
| CN |
| NA |
∵由(1)可得设BC=2,则EC=1,AC=
| 8 |
| ||
| 2 |
1-(
|
| ||
| 2 |
∴解得:
| PM |
| MA |
| CN |
| NA |
| ||||||
|
| 1 |
| 3 |
点评:本题主要考查了直线与平面平行的判定,平面与平面垂直的判定,熟练应用相关判定定理和性质定理是解题的关键,属于基本知识的考查.

练习册系列答案
相关题目
O为平行四边形ABCD所在平面上一点,若3|
|=2|
|,
+
=λ(
+
),
=μ(
+2
),则λ的值是( )
| AB |
| AD |
| OA |
| OB |
| OC |
| OD |
| OA |
| AB |
| AC |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |