题目内容
9.已知命题P:f(x)=ax-a-x是增函数,命题q:?x∈(0,+∞)使x+$\frac{1}{x}$>a,若p∨q为真,p∧q为假,求实数a的取值范围.分析 命题P:f(x)=ax-a-x是增函数,则a>1.命题q:?x∈(0,+∞),x+$\frac{1}{x}$≥2,可得2>a.若p∨q为真,p∧q为假,可得p与q必然一真一假,即可得出.
解答 解:命题P:f(x)=ax-a-x是增函数,则a>1.
命题q:?x∈(0,+∞),x+$\frac{1}{x}$≥2,∴2>a.
若p∨q为真,p∧q为假,
∴p与q必然一真一假,
∴$\left\{\begin{array}{l}{a>1}\\{a≥2}\end{array}\right.$或$\left\{\begin{array}{l}{a≤1}\\{a<2}\end{array}\right.$,
解得a≥2或a≤1,
∴实数a的取值范围是a≥2或a≤1.
点评 本题考查了简易逻辑的判定方法、不等式的解法、函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.直线y=k(x-1)+2与抛物线x2=4y的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
20.在△ABC中,若顶点B、C的坐标分别是(-a,0)和(a,0),其中a>0,G为△ABC的重心(三角形三条中线的交点),若|AG|=2,则点G的轨迹方程是( )
| A. | x2+y2=1(y≠0) | B. | x2+y2=4(y≠0) | C. | x2+y2=9(y≠0) | D. | x2+y2=a2(y≠0) |
14.已知b>a>0,ab=2,则$\frac{a^2+b^2}{a-b}$的取值范围是( )
| A. | (-∞,-4] | B. | (-∞,-4) | C. | (-∞,-2] | D. | (-∞,-2) |
1.某校高二年级有10个班,若每个班有50名同学,均随机编号1,2,…50,为了了解他们对体育运动的兴趣,要求每班第15号同学留下来进行问卷调查,这里运用的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样 | C. | 随机数表法 | D. | 有放问抽法 |
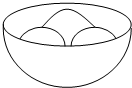 如图,三个半径均为r的小球放在一个半球形的碗中,若三个小球的最高点恰好与碗的上沿处于同一水平面.已知这个碗的半径R=3+$\sqrt{21}$,则r=3.
如图,三个半径均为r的小球放在一个半球形的碗中,若三个小球的最高点恰好与碗的上沿处于同一水平面.已知这个碗的半径R=3+$\sqrt{21}$,则r=3.