题目内容
8.写出终边在直线y=$\frac{\sqrt{3}}{3}$x上的角的集合{θ|$θ=\frac{π}{6}+kπ,k∈Z$}.分析 分别写出终边落在直线y=$\frac{\sqrt{3}}{3}$x在第一象限和第三象限两部分的集合,取并集得答案.
解答 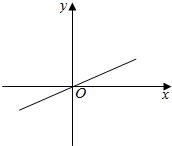 解:如图,当角的终边落在直线y=$\frac{\sqrt{3}}{3}$x在第一象限的部分时,
解:如图,当角的终边落在直线y=$\frac{\sqrt{3}}{3}$x在第一象限的部分时,
角的集合为{θ|$θ=\frac{π}{6}+2kπ,k∈Z$};
当角的终边落在直线y=$\frac{\sqrt{3}}{3}$x在第三象限的部分时,
角的集合为{θ|$θ=2kπ+π+\frac{π}{6},k∈Z$}.
∴终边在直线y=$\frac{\sqrt{3}}{3}$x上的角的集合为{θ|$θ=\frac{π}{6}+2kπ,k∈Z$}∪{θ|$θ=2kπ+π+\frac{π}{6},k∈Z$}
={θ|$θ=\frac{π}{6}+kπ,k∈Z$}.
故答案为:{θ|$θ=\frac{π}{6}+kπ,k∈Z$}.
点评 本题考查终边相同角的集合,考查并集及其运算,是基础题.

练习册系列答案
相关题目
13.“α=210°”是“sinα<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.若函数f(x)=3sin(ωx+φ)对任意实数x都有f($\frac{π}{3}$+x)=f($\frac{π}{3}$-x)恒成立,则f($\frac{π}{3}$)等于( )
| A. | 0 | B. | 3 | C. | -3 | D. | 3或-3 |
17.如图,在△ABC中,$\overrightarrow{BD}=2\overrightarrow{DC}$,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AC}=\overrightarrow b$,则$\overrightarrow{AD}$=( )
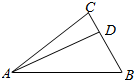

| A. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ |
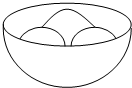 如图,三个半径均为r的小球放在一个半球形的碗中,若三个小球的最高点恰好与碗的上沿处于同一水平面.已知这个碗的半径R=3+$\sqrt{21}$,则r=3.
如图,三个半径均为r的小球放在一个半球形的碗中,若三个小球的最高点恰好与碗的上沿处于同一水平面.已知这个碗的半径R=3+$\sqrt{21}$,则r=3.