题目内容
19.已知$\vec m$=(pcosx+q,psinx),$\vec n$=(1,-$\sqrt{3}$),f(x)=$\vec m•\vec n$,△ABC的角A,B,C所对的边分别为a,b,c.(Ⅰ)若p<0时,f(x)在[0,π]上的最大值为2,最小值为-1,求p,q的值;
(Ⅱ)在(Ⅰ)的条件下,若f(A)=1,b=1,S△ABC=$\frac{{\sqrt{3}}}{2}$,求边a,角C.
分析 (I)由向量乘法可知f(x)=$\vec m•\vec n$=pcosx+q-$\sqrt{3}$psinx=-2psin(x-$\frac{π}{6}$)+q,根据x的取值范围求出sin(x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],从而求出p与q值;
(II)f(x)=2sin(x-$\frac{π}{6}$),根据f(A)与面积求出A角与c,利用余弦定理求出a与C角.
解答 解:(Ⅰ)∵$\vec m$=(pcosx+q,psinx),$\vec n$=(1,-$\sqrt{3}$),
p<0时,f(x)在[0,π]上的最大值为2,最小值为-1,
∴f(x)=$\vec m•\vec n$=pcosx+q-$\sqrt{3}$psinx=-2psin(x-$\frac{π}{6}$)+q,
∵x∈[0,π],x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$]
∴sin(x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1]
∴$\left\{\begin{array}{l}{-2p+q=2}\\{p+q=-1}\end{array}\right.$,解得p=-1,q=0.
(Ⅱ)由(Ⅰ)得f(x)=2sin(x-$\frac{π}{6}$).
∴f(A)=2sin(A-$\frac{π}{6}$)=1,
∴sin(A-$\frac{π}{6}$)=$\frac{1}{2}$
在△ABC中,A-$\frac{π}{6}$=$\frac{π}{6}$或$\frac{5π}{6}$⇒A=$\frac{π}{3}$ 或π(舍);
S△ABC=$\frac{1}{2}bcsinA$=$\frac{1}{2}×1×c×$$\frac{\sqrt{3}}{2}$=$\frac{{\sqrt{3}}}{2}$,
解得c=2;
∴a=$\sqrt{{b}^{2}+{c}^{2}-2bccosA}$=$\sqrt{3}$;
∵cosC=$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$=0;
所以,C=$\frac{π}{2}$;
综上:a=$\sqrt{3}$,C=$\frac{π}{2}$.
点评 本题主要考查了平面向量基本运算,三角函数化简与值域求法以及余弦定理的应用,属中等题.

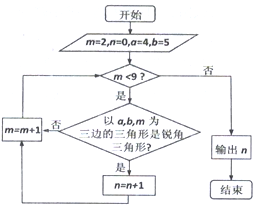
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
| A. | 向左平移$\frac{3π}{4}$个单位长度 | B. | 向右平移$\frac{3π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{3π}{16}$个单位长度 | D. | 向右平移$\frac{3π}{16}$个单位长度 |
| A. | -$\frac{1}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{7}{18}$ |
| A. | (0,1] | B. | [0,1] | C. | [-1,0) | D. | (0,+∞) |
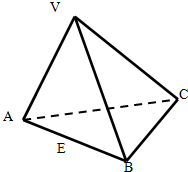 三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,E为AB边中点.
三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,E为AB边中点.