题目内容
18.如图所示,运行流程图,则输出的n的值等于( )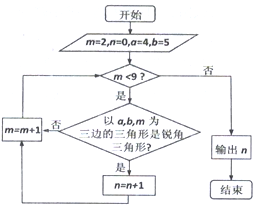
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据已知中的流程图,我们模拟程序的运行结果,首先分析程序框图,循环体为“当型“循环结构,按照循环结构进行运算,求出满足题意时及继续循环的条件是否满足,当继续循环的条件不满足时,即可得到输出结果.
解答 解:模拟程序的运行,可得:
当m=2,n=0,a=4,b=5时,执行循环
第1次循环:m=3,n=1,a=4,b=5,
第2次循环:m=4,n=1,a=4,b=5,
第3次循环:m=5,n=2,a=4,b=5,
第4次循环:m=6,n=3,a=4,b=5,
第5次循环:m=7,n=4,a=4,b=5,
第6次循环:m=8,n=4,a=4,b=5,
第7次循环:m=9,n=4,a=4,b=5,
第8次循环:m=10,n=4,a=4,b=5,
此时不满足循环条件,退出循环,输出n的值为4.
故选:C.
点评 本题考查的知识点是程序框图,模拟循环的执行过程是解答此类问题常用的办法,属于基础题.

练习册系列答案
相关题目
8.已知实数x、y、z满足x2+2y2+3z2=4,设T=xy+yz,则T的取值范围是( )
| A. | [$-\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$] | B. | [$-\frac{\sqrt{6}}{6}$,$\frac{2\sqrt{6}}{3}$] | C. | [$-\frac{\sqrt{6}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | [$-\frac{2\sqrt{6}}{3}$,$\frac{2\sqrt{6}}{3}$] |
9.已知f($\frac{1-x}{1+x}$)=$\frac{1-{x}^{2}}{1+{x}^{2}}$,则f(x)的解析式可取为( )
| A. | $\frac{x}{1+{x}^{2}}$ | B. | -$\frac{2x}{1+{x}^{2}}$ | C. | $\frac{2x}{1+{x}^{2}}$ | D. | -$\frac{x}{1+{x}^{2}}$ |
13.已知等差数列{an}的前n项和为Sn,公差为2,且a1,S2,S4成等比数列,则数列{an}的通项公式an等于( )
| A. | 2n+1 | B. | 2n-3 | C. | 2n-1 | D. | 2n |
3.命题“?x∈R,x2-4<0或x2-4x>0”的否定为( )
| A. | ?x∈R,x2-4≥0或x2-4x≤0 | B. | ?x∈R,x2-4≥0且x2-4x≤0 | ||
| C. | ?x∈R,x2-4≥0或x2-4x≤0 | D. | ?x∈R,x2-4≥0且x2-4x≤0 |
7.已知函数f(x)=-x3+ax2-x-1在R上不是单调函数,则实数a的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) |