Question

4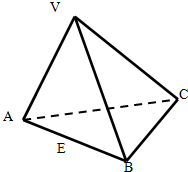．三棱锥V-ABC中，VA=VB=AC=BC=2，AB=2$\sqrt{3}$，VC=1，E为AB边中点．
（1）求证：AB⊥平面VEC；
（2）求出二面角V-AB-C的大小．

Answer 1

分析 （1）连接VE，CE．利用等腰三角形的性质可得：VE⊥AB，CE⊥AB，于是AB⊥平面CEV，即可证明AB⊥VC．
（2）VA=VB，可得AB⊥VE；同理AB⊥CE．可得∠VEC是二面角V-AB-C的平面角． 利用等边三角形的性质即可得出．

解答 （1）证明：连接VE，CE．
∵VA=VB，AC=BC，∴VE⊥AB，CE⊥AB．
∵VE∩CE=E，∴AB⊥平面CEV，
∵VC?平面CEV，
∴AB⊥VC．
（2）解：∵VA=VB，∴AB⊥VE；
同理AB⊥CE．
∴∠VEC是二面角V-AB-C的平面角．
由题设可知VE=CE=1，即∠VEC=60°．
故二面角V-AB-C的大小为60°．

点评 本题考查了等腰三角形的性质、线面垂直的判定与性质定理、二面角，考查了推理能力与计算能力，属于中档题．