题目内容
已知向量
=(2cosωx,2),
=(2cos(ωx+
),0)(ω>0),函数f(x)=
•
的图象与直线y=-2+
的相邻两个交点之间的距离为π.
(Ⅰ)求函数f(x)在[0,2π]上的单调递增区间;
(Ⅱ)将函数f(x)的图象向右平移
个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有6个零点,求b的最小值.
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
(Ⅰ)求函数f(x)在[0,2π]上的单调递增区间;
(Ⅱ)将函数f(x)的图象向右平移
| π |
| 12 |
考点:函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算
专题:三角函数的图像与性质,平面向量及应用
分析:(I)运用向量的数量积的坐标表示以及二倍角公式和两角和的余弦公式,化简f(x),再由余弦函数的周期和单调增区间,解不等式即可得到;
(II)由图象变换的特点,可得y=g(x),令g(x)=0,求得零点,每个周期恰有2个零点,要恰有6个零点,则b不小于6个零点的横坐标即可.
(II)由图象变换的特点,可得y=g(x),令g(x)=0,求得零点,每个周期恰有2个零点,要恰有6个零点,则b不小于6个零点的横坐标即可.
解答:
解:(I)由于向量
=(2cosωx,2),
=(2cos(ωx+
),0)(ω>0),
f(x)=
•
=4cosωxcos(ωx+
)=4cosωx(
cosωx-
sinωx)
=2
•
-sin2ωx,
即有f(x)=2cos(2ωx+
)+
,
由题意得T=π,所以ω=1,所以f(x)=2cos(2x+
)+
,
由2x+
∈[2kπ-π,2kπ],解得x∈[kπ-
,kπ-
],
又x∈[0,2π],则所求单调增区间为[
,
]和[
,
];
(II)由题意得y=g(x)=2cos2x+
,
令g(x)=0得x=kπ+
或x=kπ+
,k∈Z,
每个周期恰有2个零点,要恰有6个零点,
则b不小于6个零点的横坐标即可,
即bmin=2π+
=
.
| a |
| b |
| π |
| 6 |
f(x)=
| a |
| b |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
=2
| 3 |
| 1+cos2ωx |
| 2 |
即有f(x)=2cos(2ωx+
| π |
| 6 |
| 3 |
由题意得T=π,所以ω=1,所以f(x)=2cos(2x+
| π |
| 6 |
| 3 |
由2x+
| π |
| 6 |
| 7π |
| 12 |
| π |
| 12 |
又x∈[0,2π],则所求单调增区间为[
| 5π |
| 12 |
| 11π |
| 12 |
| 17π |
| 12 |
| 23π |
| 12 |
(II)由题意得y=g(x)=2cos2x+
| 3 |
令g(x)=0得x=kπ+
| 5π |
| 12 |
| 7π |
| 12 |
每个周期恰有2个零点,要恰有6个零点,
则b不小于6个零点的横坐标即可,
即bmin=2π+
| 7π |
| 12 |
| 31π |
| 12 |
点评:本题考查向量的数量积的坐标运算以及二倍角公式和两角和的余弦公式的运用,主要考查余弦函数的周期公式和单调性和图象变换,以及零点的判断,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
若向量
、
满足
+
=(2,-1),
=(1,2),则向量
与
的夹角等于( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、135° | B、120° |
| C、60° | D、45° |
若-
<α<-
,从单位圆中的三角函数线观察sinα,cosα,tanα的大小是( )
| 3π |
| 4 |
| π |
| 2 |
| A、sinα<tanα<cosα |
| B、cosα<sinα<tanα |
| C、sinα<coasα<tanα |
| D、tanα<sinα<cosα |
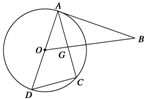 如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.求证:BA•DC=GC•AD.
如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.求证:BA•DC=GC•AD. 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积为
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积为