题目内容
已知|
|=12,|
|=9,
•
=-54
,则
与
的夹角为 .
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:运用向量的数量积的定义,结合向量夹角的范围和特殊角的三角函数值,即可得到.
解答:
解:由|
|=12,|
|=9,
•
=-54
,
可得
•
=12×9cos<
,
>=-54
,
即cos<
,
>=-
,
由0≤<
,
>≤π,
则有
与
的夹角为
.
故答案为:
.
| a |
| b |
| a |
| b |
| 2 |
可得
| a |
| b |
| a |
| b |
| 2 |
即cos<
| a |
| b |
| ||
| 2 |
由0≤<
| a |
| b |
则有
| a |
| b |
| 3π |
| 4 |
故答案为:
| 3π |
| 4 |
点评:本题考查向量的数量积的定义和夹角的求法,熟记特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
已知O是△ABC所在平面内一点,且|
|2+|
|2=|
|2+|
|2=|
|2+|
|2,则O是△ABC的( )
| OC |
| AB |
| OB |
. |
| AC |
| OA |
| BC |
| A、内心 | B、垂心 | C、外心 | D、重心 |
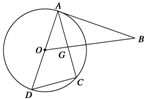 如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.求证:BA•DC=GC•AD.
如图,已知AD为⊙O的直径,直线BA与⊙O相切于点A,直线OB与弦AC垂直并相交于点G.求证:BA•DC=GC•AD.