题目内容
已知C点在⊙O直径BE的延长线上，CA切⊙O于A点，若AB=AC，则
= ．
| AB |
| BC |
考点：与圆有关的比例线段
专题：推理和证明
分析：由已知得C=∠B=∠CAE，从而∠AEB=2∠B=60°，设圆半径为r，则AE=CE=r，BC=3r，AC=AB=
r，由此能求出
的值．
| 3 |
| AC |
| BC |
解答：
解：∵C点在⊙O直径BE的延长线上，
CA切⊙O于点A，AB=AC，
∴∠C=∠B=∠CAE，∴∠AEB=2∠B=60°，
设圆半径为r，
则AE=CE=r，BC=3r，AC=AB=
r，
∴
=
．
故答案为：
．
CA切⊙O于点A，AB=AC，
∴∠C=∠B=∠CAE，∴∠AEB=2∠B=60°，
设圆半径为r，
则AE=CE=r，BC=3r，AC=AB=
| 3 |
∴
| AC |
| BC |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查与圆相关的两数比值的求法，是中档题，解题时要注意弦切角定理、圆的简单性质的合理运用．
练习册系列答案
相关题目
已知O是△ABC所在平面内一点，且|
|2+|
|2=|
|2+|
|2=|
|2+|
|2，则O是△ABC的（ ）
| OC |
| AB |
| OB |
. |
| AC |
| OA |
| BC |
| A、内心 | B、垂心 | C、外心 | D、重心 |
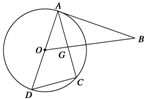如图，已知AD为⊙O的直径，直线BA与⊙O相切于点A，直线OB与弦AC垂直并相交于点G．求证：BA•DC=GC•AD．一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、8+
| ||||
B、8+2
| ||||
| C、12 | ||||
D、
|