题目内容
已知直线y=
x与抛物线y2=2px(p>0)交于O,A两点(F为抛物线的焦点,O为坐标原点),若|AF|=17,求OA的垂直平分线的方程.
| 1 |
| 2 |
考点:直线与圆锥曲线的关系
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求焦点F的坐标为(0.5p,0),再求得A坐标(4p,8p),从而有(4p-0.5p)2+(8p-0)2=AF2=172,可解得p的值,从而可求OA的垂直平分线的方程.
解答:
解:由题意可得:F(0.5p,0),
由y=
,得:x=2y,
可得:y2=2px=2p•2y,
∴可得:y=4p,x=8p,
∴可得:A(8p,4p),
∴(4p-0)2+(8p-0.5p)2=AF2=172,
∴72.25p2=172,
∵p>0,∴可解得:p=2,
∴OA的垂直平分线的方程是:y-4p=-2•(x-2p),
即y-4=-2•(x-8).
化简后一般式为:2x+y-20=0.
由y=
| x |
| 2 |
可得:y2=2px=2p•2y,
∴可得:y=4p,x=8p,
∴可得:A(8p,4p),
∴(4p-0)2+(8p-0.5p)2=AF2=172,
∴72.25p2=172,
∵p>0,∴可解得:p=2,
∴OA的垂直平分线的方程是:y-4p=-2•(x-2p),
即y-4=-2•(x-8).
化简后一般式为:2x+y-20=0.
点评:本题考查抛物线的几何性质,考查直线与圆锥曲线的关系,考查学生分析解决问题的能力,考查了转化思想.

练习册系列答案
相关题目
已知异面直线a,b均与平面α相交,下列命题:
(1)存在直线m?α,使得m⊥a或m⊥b.
(2)存在直线m?α,使得m⊥a且m⊥b.
(3)存在直线m?α,使得m与a和b所成的角相等.
其中不正确的命题个数为( )
(1)存在直线m?α,使得m⊥a或m⊥b.
(2)存在直线m?α,使得m⊥a且m⊥b.
(3)存在直线m?α,使得m与a和b所成的角相等.
其中不正确的命题个数为( )
| A、0 | B、1 | C、2 | D、3 |
设a=log3π,b=log2
,c=log3
,则( )
| 3 |
| 2 |
| A、a>c>b |
| B、b>c>a |
| C、b>a>c |
| D、a>b>c |
已知集合A={x||x-1|<2},集合B={x|lnx>0},则集合A∩B=( )
| A、(1,3) |
| B、(0,3) |
| C、(-1,3) |
| D、(-1,1) |
 如图,双曲线
如图,双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、1+
| ||
B、4+2
| ||
C、2
| ||
D、2
|
如图,阴影部分的面积是( )
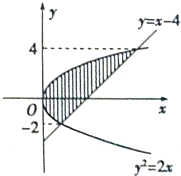

| A、16 | B、18 | C、20 | D、22 |
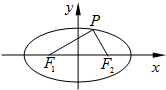 已知点P(m,4)是椭圆
已知点P(m,4)是椭圆