题目内容
已知函数f(x)=
x3+3xf′(a),f(a)=
,则a= .
| 1 |
| 3 |
| 7 |
| 6 |
考点:导数的运算,函数的零点
专题:导数的概念及应用
分析:求函数的导数,建立方程进行求解即可.
解答:
解:函数的f(x)的导数f′(x)=x2+3f′(a),
则f′(a)=a2+3f′(a),
解得f′(a)=-
a2,
则f(x)=
x3-
a2x,
∵f(a)=
,
∴f(a)=
a3-
a3=
,
即-
a3=
,
a3=-1,
解得a=-1,
故答案为:-1
则f′(a)=a2+3f′(a),
解得f′(a)=-
| 1 |
| 2 |
则f(x)=
| 1 |
| 3 |
| 3 |
| 2 |
∵f(a)=
| 7 |
| 6 |
∴f(a)=
| 1 |
| 3 |
| 3 |
| 2 |
| 7 |
| 6 |
即-
| 7 |
| 6 |
| 7 |
| 6 |
a3=-1,
解得a=-1,
故答案为:-1
点评:本题主要考查导数的计算,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
下列函数中,既是偶函,又在[0,1]上单调递增的是( )
| A、y=cosx |
| B、y=-x2 |
| C、y=sinxcos2x |
| D、y=|sinx| |
已知向量
=(2x,1),向量
=(-4,2),若
∥
,则
+
为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(-2,2) |
| B、(-6,3) |
| C、(2,-1) |
| D、(6,-3) |
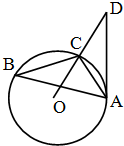 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD切圆O于A,若∠ABC=30°,AC=2,则AD的长为