题目内容

已知函数f（x）=|2x-a|+a（a＞0），若f（x）+f（-x）＜4有解，求a的取值范围．
考点：分段函数的应用
专题：计算题,函数的性质及应用
分析：化简f（x）=|2x-a|+a=
2x，x≥
a
2
2a-2x，x＜
a
2
，从而讨论化简f（x）+f（-x）＜4有解，从而求解．
解答： 解：f（x）=|2x-a|+a=
2x，x≥
a
2
2a-2x，x＜
a
2
，
①若有解在x≥
a
2
上，则
f（x）+f（-x）=2x+2a+2x＜4；
故4x+2a＜4；
故4×
a
2
+2a＜4；
故a＜1；
②若有解在x＜
a
2
上，则
f（x）+f（-x）=2a-2x+2a+2x=4a＜4；
故a＜1；
综上所述，
a的取值范围为（0，1）．
点评：本题考查了分段函数的化简与不等式中的应用，同时考查了存在性命题，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=lnx+
1-x
a(1+x)
，其中a为不为零的常数．
（Ⅰ）若f（x）在点（1，0）处的切线过点（2，-1），求实数a的值；
（Ⅱ）当a=1时，若存在x1，x2∈[1，e2]使得f（x1）-f（x2）≥M成立，求满足条件的最大整数M；
（Ⅲ）若f（x）无极值，求实数a的取值范围．
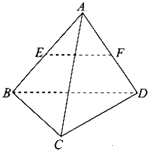如图，四面体ABCD的每条棱长都等于2，点E，F分别为棱AB，AD的中点，则|
AB
+
BC
|=
 
，|
BC
-
EF
|=
 
，
EF
与
AC
所成的角为
 
．
若曲线y=
1
xlnx
与直线y=a恰有一个公共点，则实数a的取值范围为
 
．
“世界睡眠日”定在每年的3月21日．为此某网站2014年3月13日到3月20日持续一周进行了睡眠时间的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示，
（Ⅰ） 在答题卡给定的坐标系中画出频率分布直方图（如图1）；
（Ⅱ）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．
序号
（i）		分组睡
眠时间		组中值
（mi）		频数
（人数）		频率
（fi）
1[4，5）4.580.04
2[5，6）5.5520.26
3[6，7）6.5600.30
4[7，8）7.5560.28
5[8，9）8.5200.10
6[9，10]9.540.02
已知A（3，0，1），B（0，3，-2），则直线AB与平面xOy的交点C的坐标为
 
．
在平面直角坐标系xOy中，直线l的参数方程为
x=2+2t
y=1-t
（t为参数），椭圆C的方程为
x2
4
+y2=1，试在椭圆C上求一点P，使得P到直线l的距离最小．
已知
a
，
b
为平面向量，若
a
+
b
与
a
的夹角为60°，
a
+
b
与
b
的夹角为45°，则|
a
|与|
b
|之比为（　　）
A、
3
3
B、
5
3
C、
6
3
D、
6
2
已知过抛物线y2=2px（p＞0）的焦点的直线交抛物线于A、B两点，且|AB|=
5
2
p，求AB所在的直线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网